Texas Instruments (TI) Calculators for Linear Models

You may use any of these TI calculators:
TI-83 Plus
TI-84 Plus series
TI-Nspire CX series
TI-89 Titanium
TI-73 Explorer

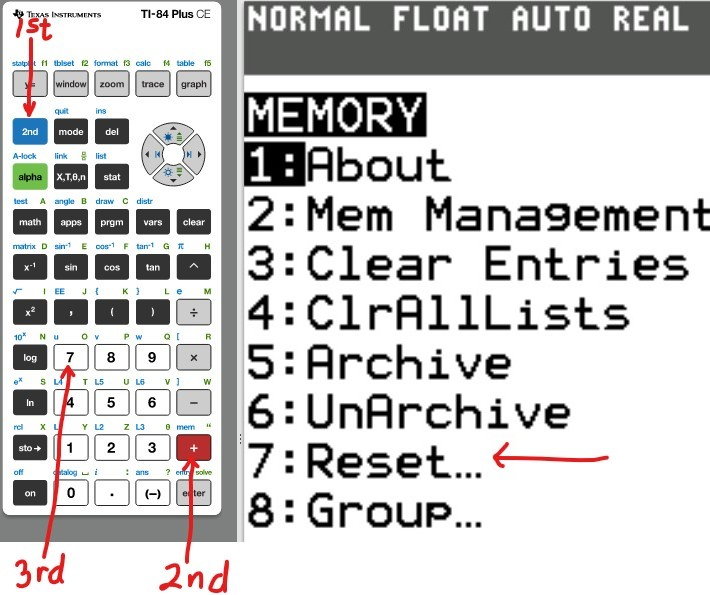
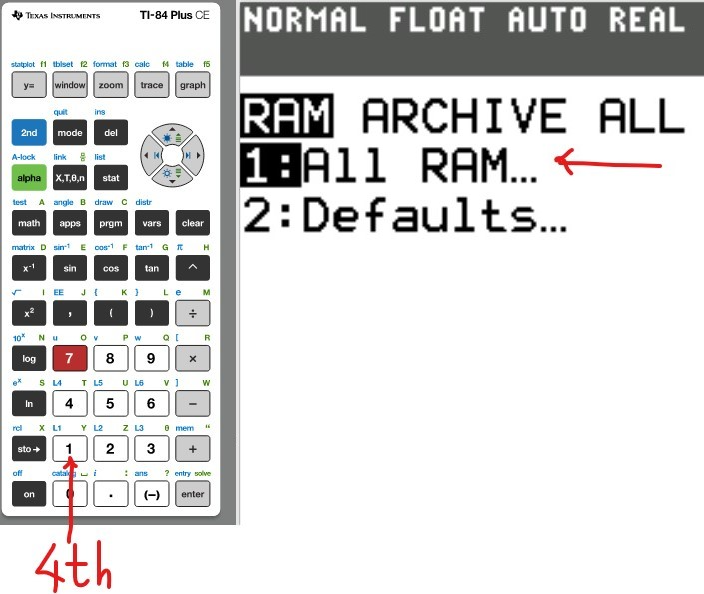
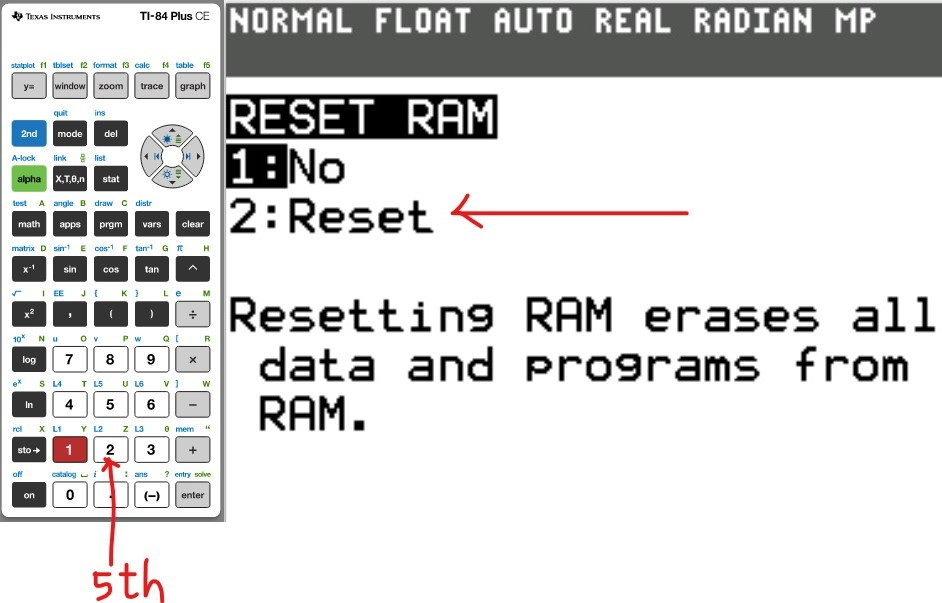
The first thing we need to do is to reset the Random Access Memory (RAM).
This will clear everything that was initially stored by a previous user.
Also, after each problem, it is recommended that you reset the calculator.

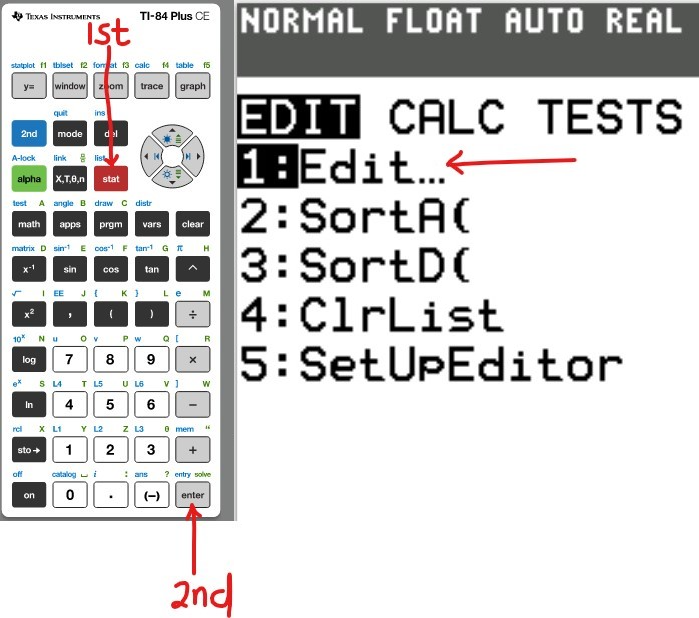
Reset the Calculator
(1.) Reset 1

(2.) Reset 2

(3.) Reset 3

(4.) Reset 4

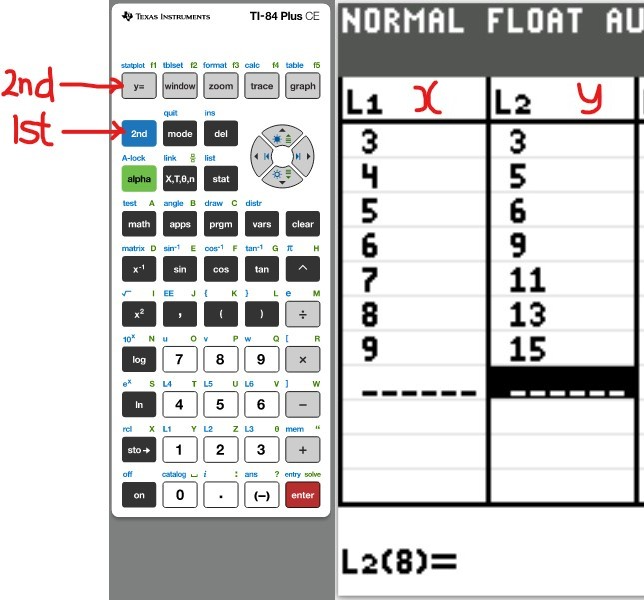
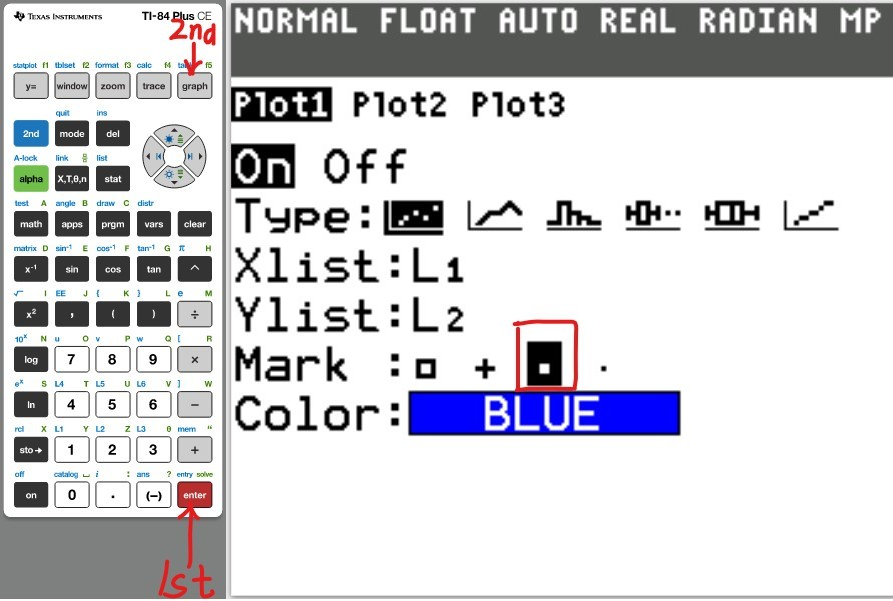
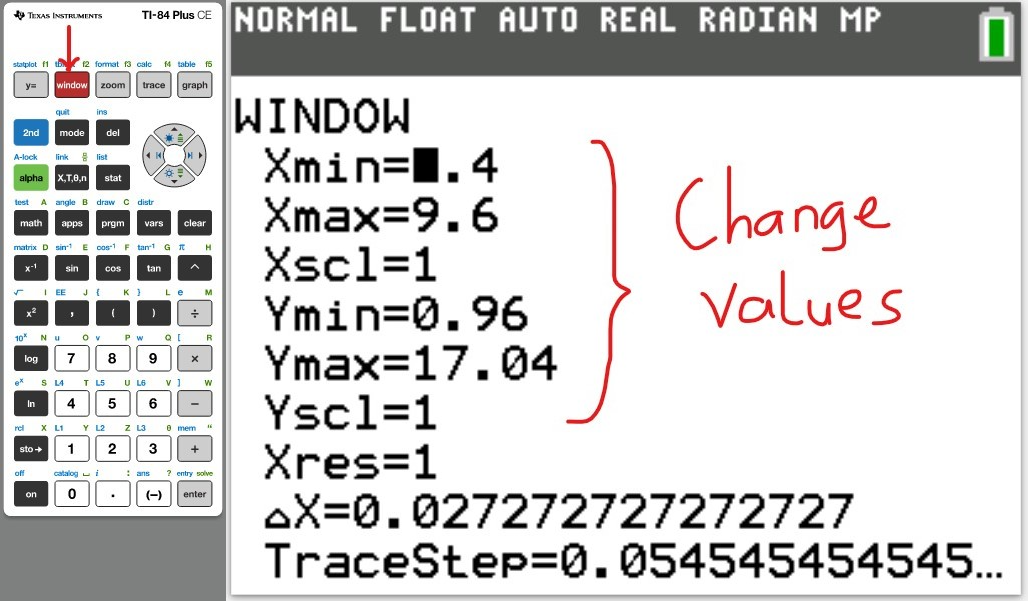
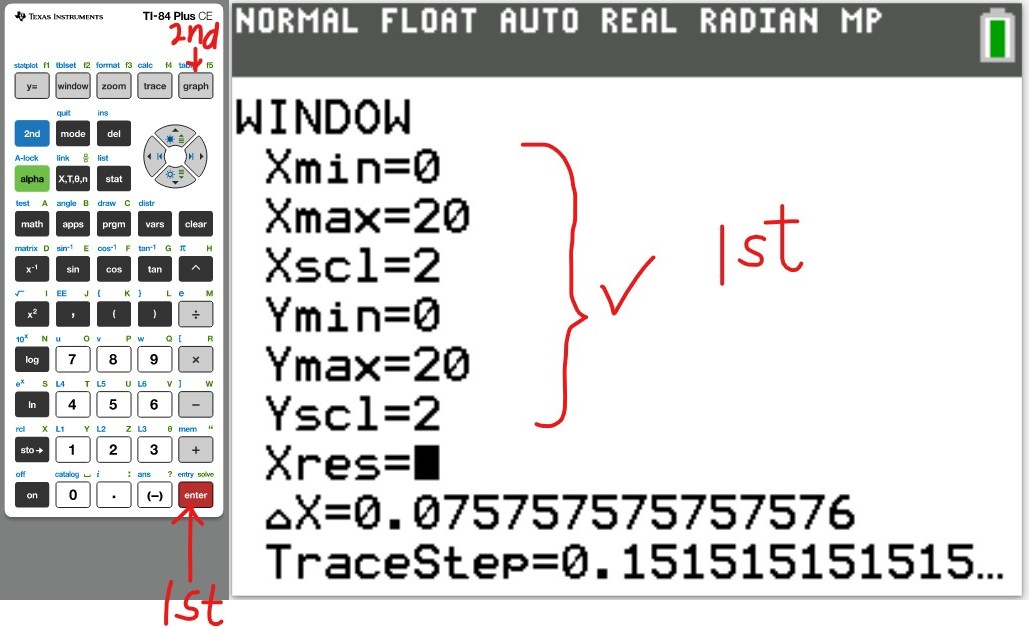
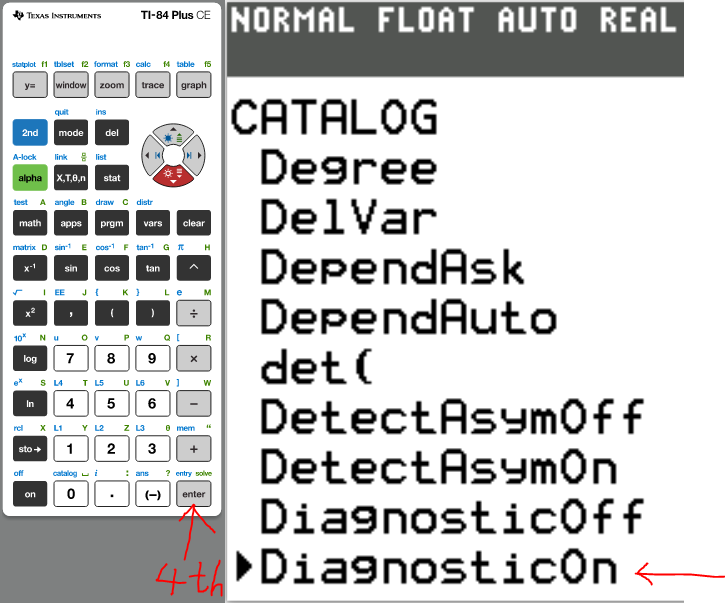
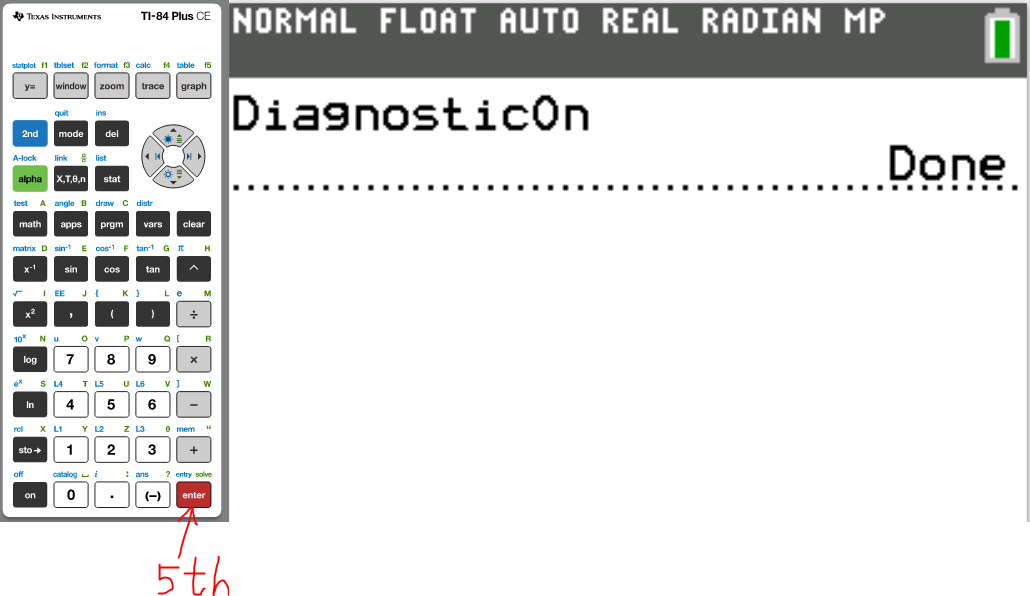
Set up the Calculator
The first thing we need to do is to turn Diagonstic On

(1.) Set Up 1

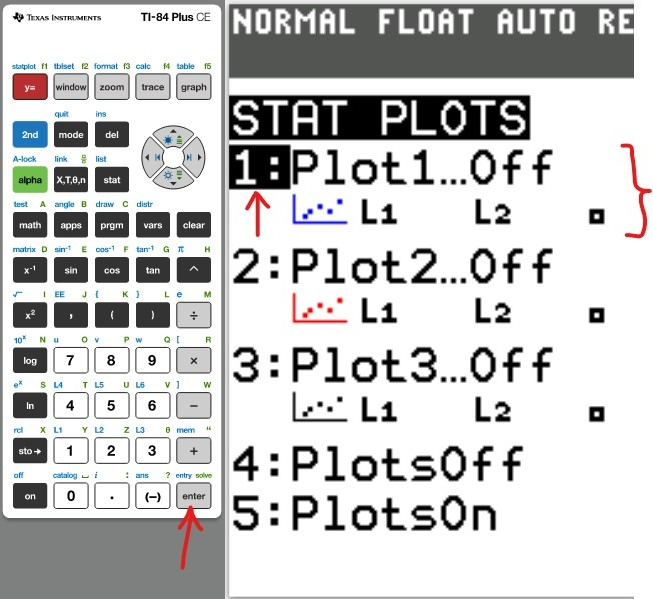
(2.) Set Up 2

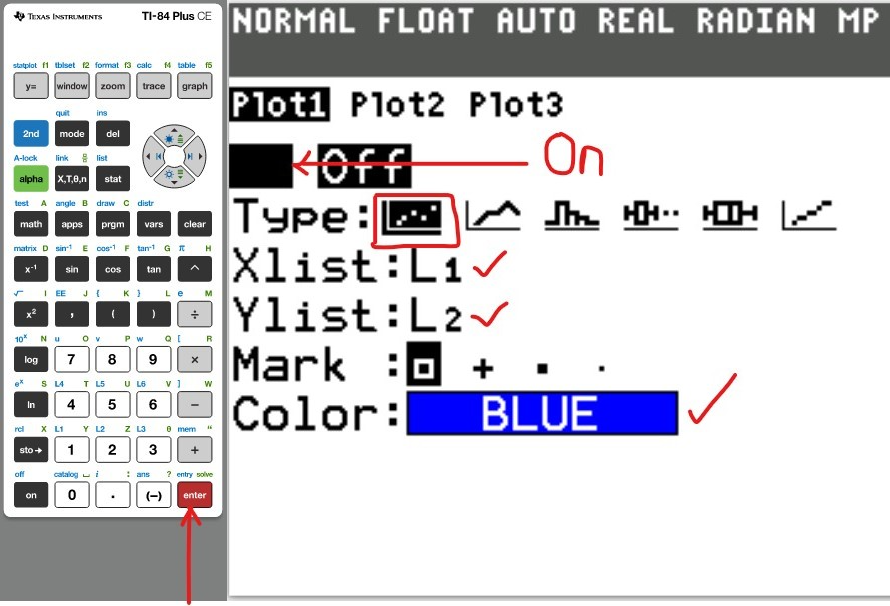
(3.) Set Up 3

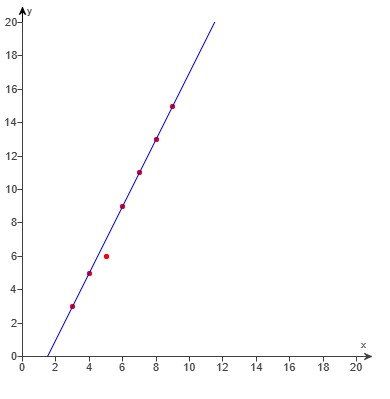
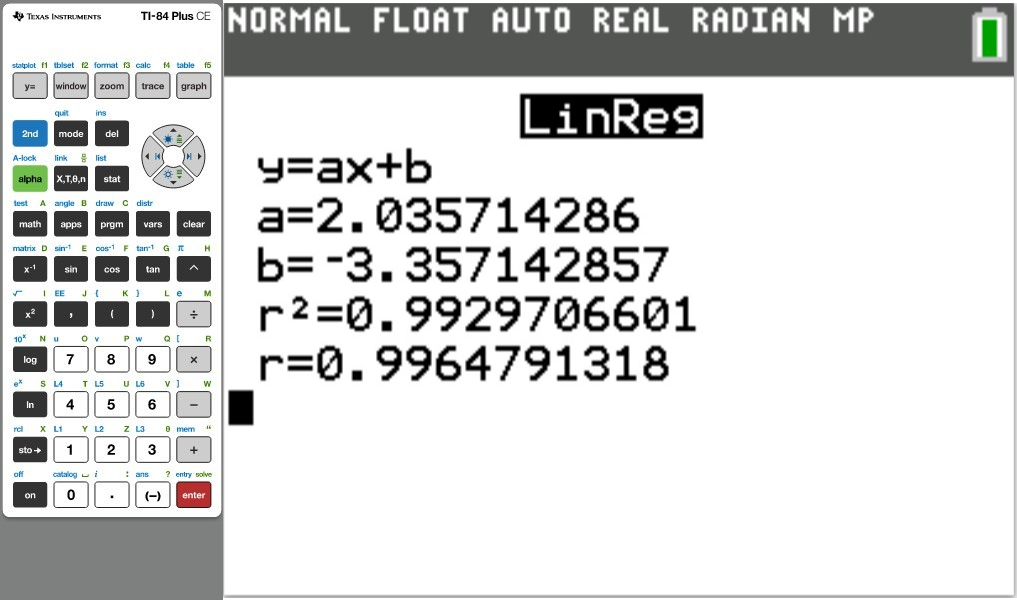
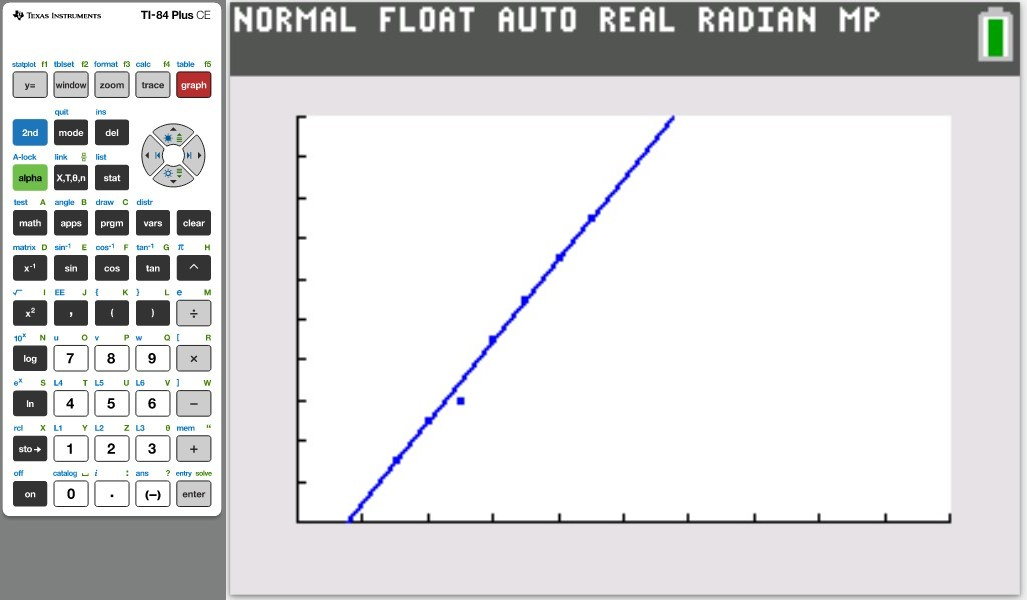
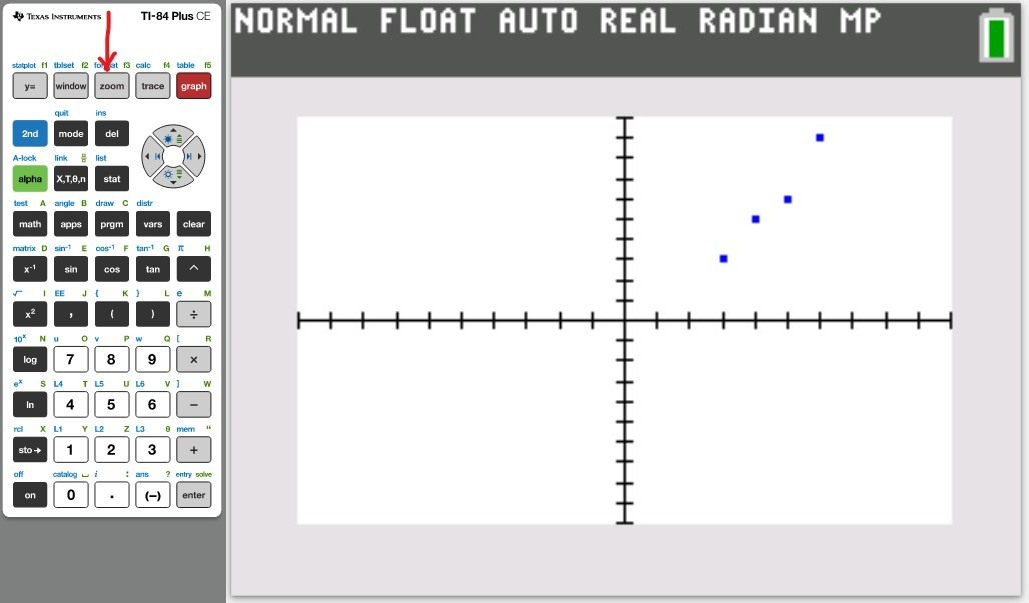
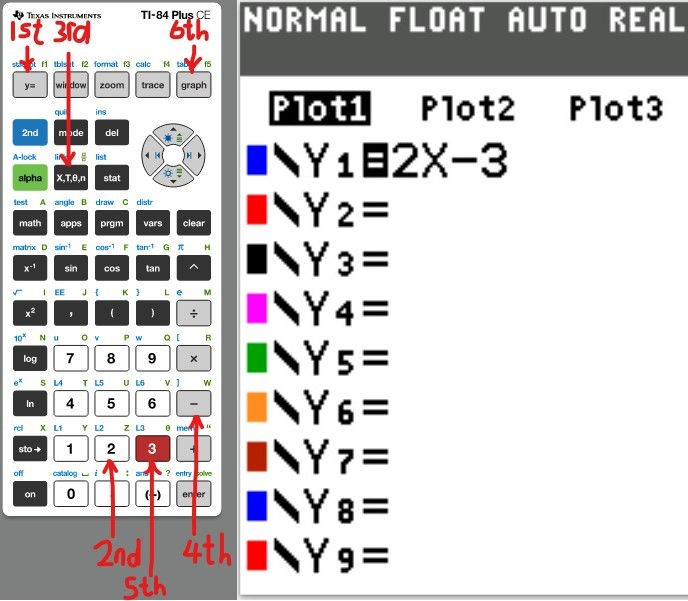
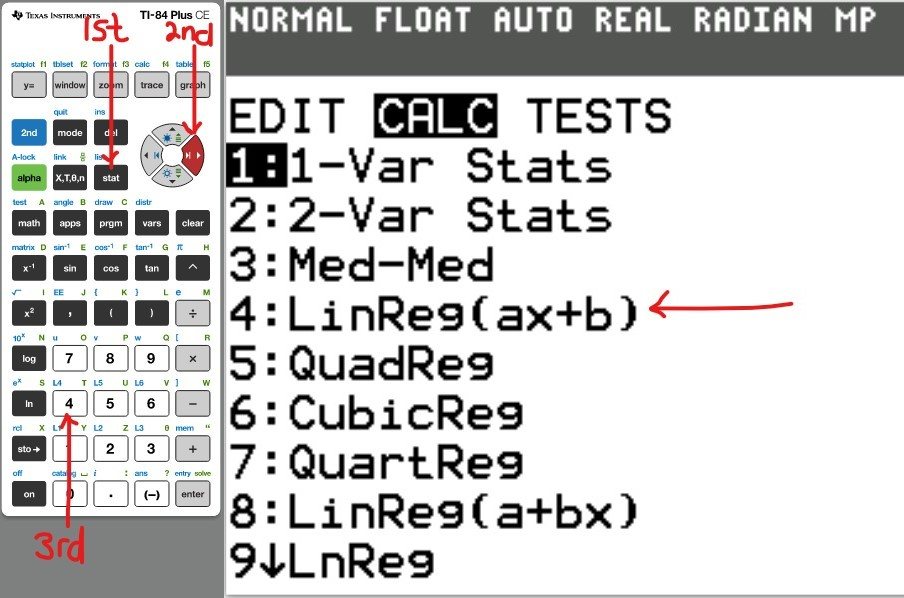
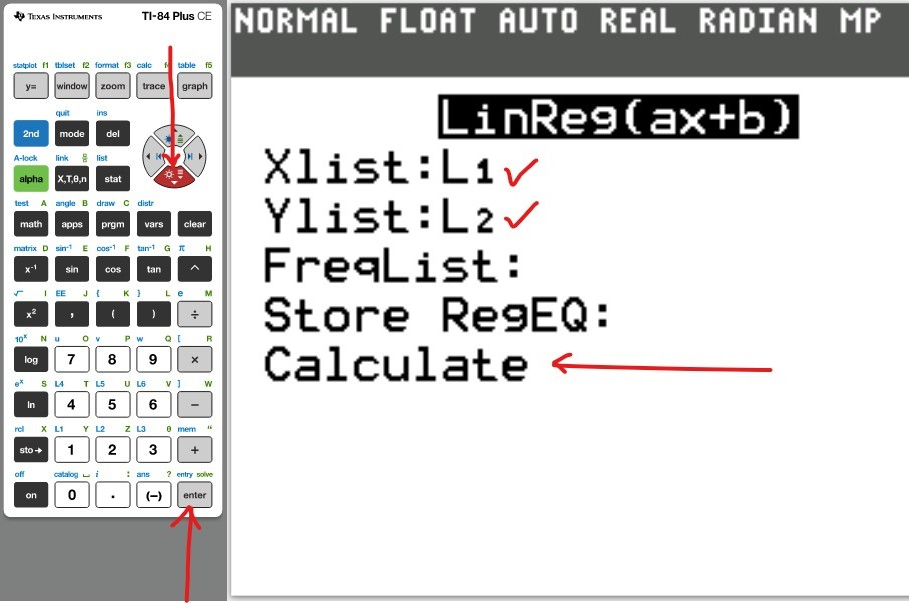
Let us do some examples.
NOTE: Please begin from the first example. Do not skip.

Concept: Scatter Diagrams; Line of Best Fit; Correlation Coefficient
(a.) Draw scatter diagram of a given dataset.
(b.) Graph a straight line equation on the scatter diagram.
(c.) Determine the line of best fit (regression equation line) of the dataset.
(d.) Determine the correlation coefficient of the dataset.

(1.) For the data given below:

x	3	4	5	6	7	8	9
y	3	5	6	9	11	13	15

(a.) Choose the correct graph.

Number 1a

(b.) Graph the line: y = 2x − 3 on the scatter plot.
Choose the correct graph.

Number 1b

(c.) Use a graphing utility to find the line of best fit.
Type integers or decimals rounded to four decimal places as needed.

(d.) What is the correlation coefficient, r?
Type an integer or decimal rounded to three decimal places as needed.

(e.) Use a graphing utility to draw the scatter plot and graph the line of best fit on it using these values:
Xmin = 0, Xmax = 20, Xscl = 2, Ymin= 0, Ymax = 20, Yscl = 2
Choose the correct graph.

Number 1e

(a.) The scatter diagram is:
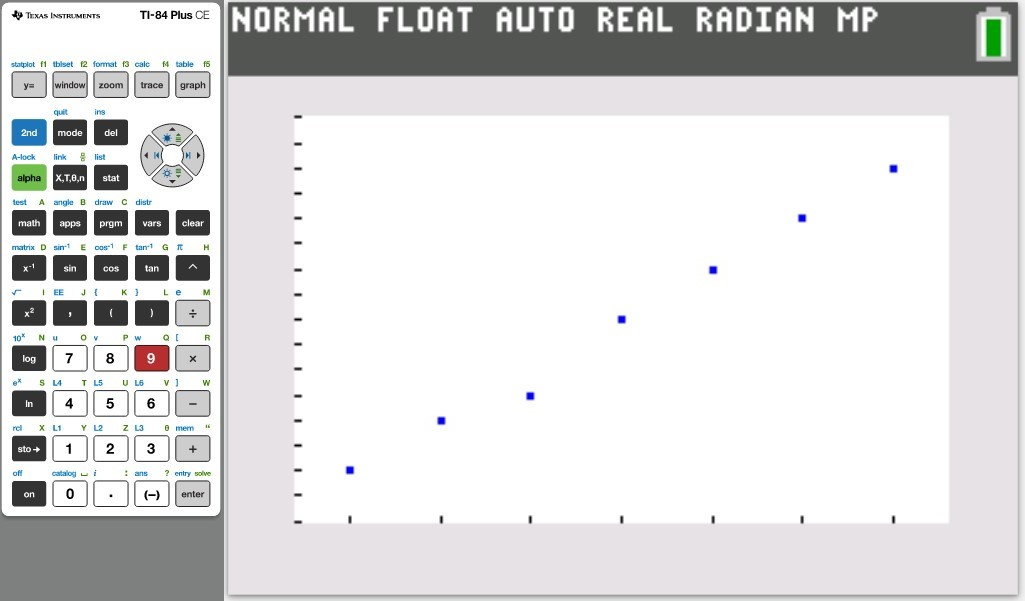
Scatter Diagram 8

Based on it, the correct answer is Option A.
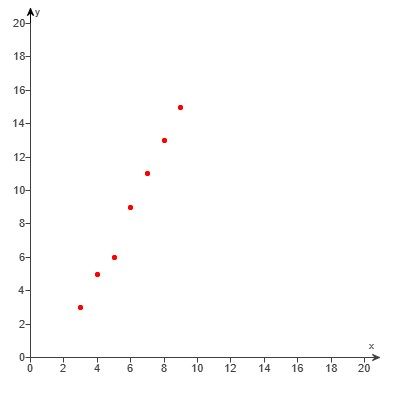
Number 1a

(b.) The graph of the linear equation is:
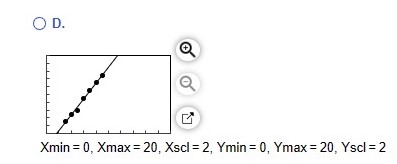
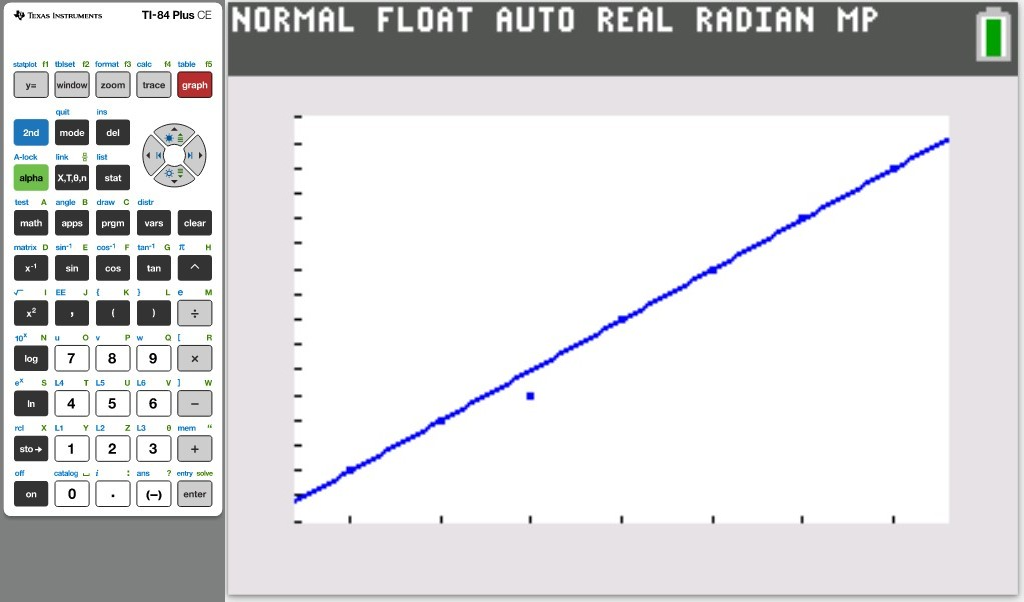Graph Linear Equations 2

Based on it, the correct answer is also Option A.
Number 1b

(c.) The line of best fit (regression equation line) is:
Regression Equation 3

$ y = ax + b \\[3ex] y = 2.035714286x - 3.357142857 \\[3ex] y \approx 2.0357x - 3.3571 \\[5ex] (d.) \\[3ex] r = 0.9964791318 \\[3ex] r \approx 0.996 \\[3ex] $ (e.) The scatter plot and the line of best fit on it using these values: Xmin = 0, Xmax = 20, Xscl = 2, Ymin= 0, Ymax = 20, Yscl = 2 is:
Window 3

Based on it, the correct answer is Option D.
Number 1e

(a.) Draw scatter diagrams
(1.) Scatter Diagram 1

(2.) Scatter Diagram 2

(3.) Scatter Diagram 3

(4.) Scatter Diagram 4

(5.) Scatter Diagram 5

(6.) Scatter Diagram 6

(7.) Scatter Diagram 7

(8.) Scatter Diagram 8

(b.) Graph a straight line equation on the scatter diagram.
(1.) Graph Linear Equations 1

(2.) Graph Linear Equations 2

(c.) Use a graphing utility to find the line of best fit.
(1.) Regression Equation 1

(2.) Regression Equation 2

(3.) Regression Equation 3

(e.) Use a graphing utility to draw the scatter plot and graph the line of best fit on it using these values:
Xmin = 0, Xmax = 20, Xscl = 2, Ymin= 0, Ymax = 20, Yscl = 2
(1.) Window 1

(2.) Window 2

(3.) Window 3