is nonnegative.
Simplify your answer. Type an integer or decimal.
Simplify your answer. Type an integer or decimal.
Simplify your answer. Type an integer or decimal.
(g.) What price should the company charge to earn at least
Simplify your answer. Type an integer or decimal.
$
(a.) \\[3ex]
R(p) = x * p \\[3ex]
= p * x \\[3ex]
= p(-9p + 900) \\[3ex]
= -9p^2 + 900p \\[3ex]
$
(b.) The revenue cannot be negative.
The revenue can be zero (no revenue)
The revenue can be positive
Hence, the revenue must be nonnegative
The domain of
R includes all the real number prices such that the revenue is nonnegative
$
R(p) \ge 0 \\[3ex]
-9p^2 + 900p \ge 0 \\[3ex]
-9(p^2 - 100p) \ge 0 \\[3ex]
p^2 - 100p \le \dfrac{0}{-9} \\[5ex]
p^2 - 100p \le 0 \\[3ex]
p(p - 100) \le 0 \\[3ex]
Assume:\;\;p(p - 100) = 0 \\[3ex]
p = 0 \;\;\;OR\;\;\; p - 100 = 0 \\[3ex]
p = 0 \;\;\;OR\;\;\; p = 100 \\[3ex]
Test\;\;Intervals\;\;are: \\[3ex]
p \lt 0 \\[3ex]
0 \le p \le 100 \\[3ex]
p \gt 100 \\[3ex]
$
Let:
|
p < 0
p = −1
|
0 ≤ p ≤ 100
p = 1
|
p > 100
p = 101
|
| $p$ |
− |
+ |
+ |
| $p - 100$ |
− |
− |
+ |
| $p(p - 100)$ |
+ |
− |
+ |
Less than or equal to zero
means nonnegative
Hence, the second test interval gives the solution of the inequality
Domain, D = {p | 0 ≤ p ≤ 100}
(c.) The price that maximizes revenue is the
x-coordinate of the vertex of the revenue function.
$
R(p) = -9p^2 + 900p \\[3ex]
Compare:\;\;R(p) = ap^2 + bp + c \\[3ex]
a = -9 \\[3ex]
b = 900 \\[3ex]
x-coordinate\;\;of\;\;vertex = -\dfrac{b}{2a} \\[5ex]
p = \dfrac{-900}{2(-9)} \\[5ex]
= \dfrac{-900}{-18} \\[5ex]
= 50 \\[3ex]
$
The price that maximizes revenue is
$50
(d.) The maximum revenue is the
y-coordinate of the vertex of the revenue function.
$
R(p) = -9p^2 + 900p \\[3ex]
p = \$50 \\[3ex]
y-coordinate\;\;of\;\;vertex = R(50) \\[3ex]
R(50) = -9(50)^2 + 900(50) \\[3ex]
= -9(2500) + 45000 \\[3ex]
= -22500 + 45000 \\[3ex]
= 22500 \\[3ex]
$
The maximum revenue is
$22,500
(e.) The number of units sold at this price is the value of
x for which
R =
$22500
$
vertex = (x, y) = (p, R) = (50, 22500) \\[3ex]
R = xp \\[3ex]
xp = R \\[3ex]
x = \dfrac{R}{p} \\[5ex]
x = \dfrac{22500}{50} \\[5ex]
x = 450 \\[3ex]
$
450 units were sold at the price that gave the maximum revenue.
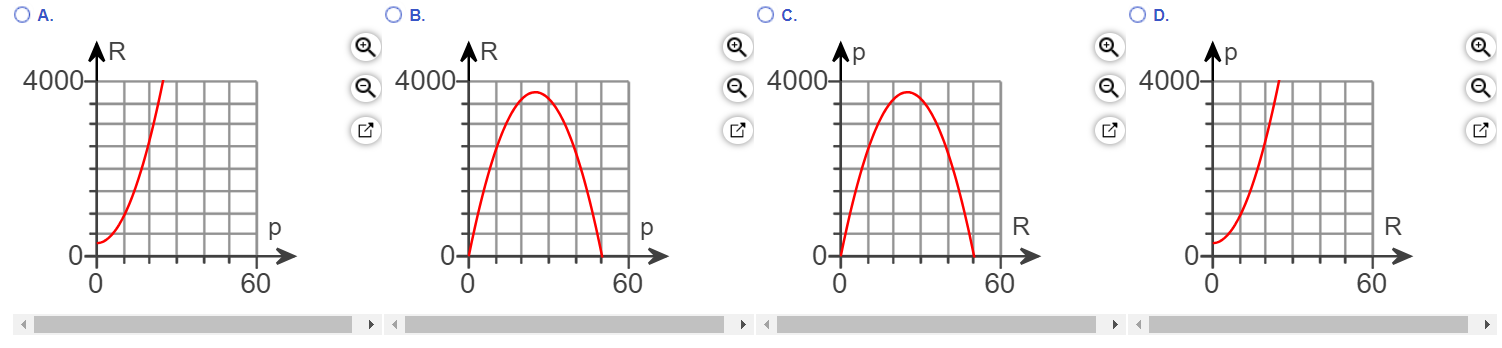
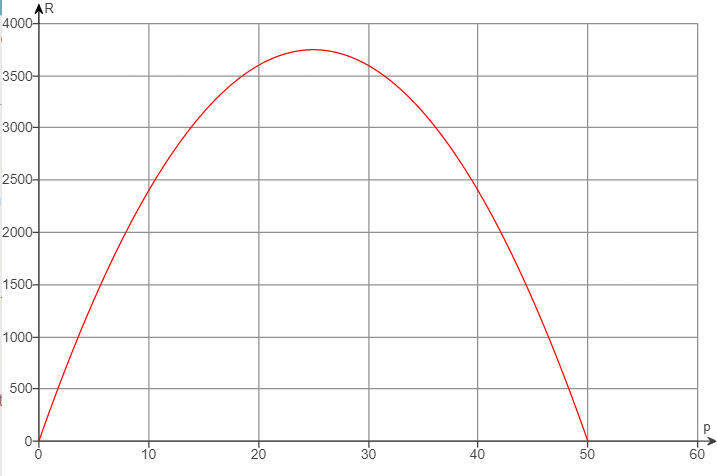
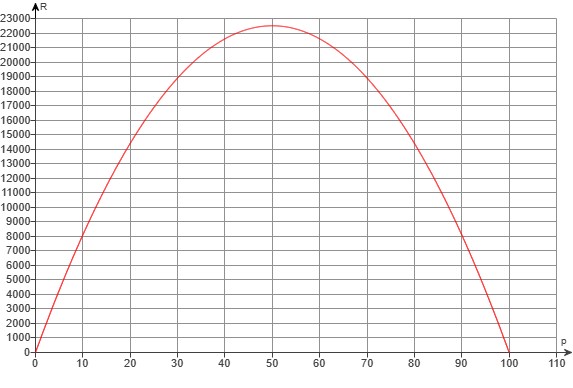
(f.) The graph of the revenue versus price is shown below.
Keep in mind that the vertex is (
p,
R) = (50, 22500)
Options (A.) and (D.) are similar.
However, option (A.) is the graph of
R versus
p while option (D.) is the graph of
p versus
R
The revenue,
R is the
y-axis
The price that maximizes the revenue,
p is the
x-axis
So, the correct graph should be the graph of
R versus
p: option (A.)
(g.) The price that the company should charge to earn at least
$10,179
At least 10179 means ≥ 10179
They are asking us to determine the price range for which the revenue is greater than or equal to
$10,179
$
-9p^2 + 900p \ge 10179 \\[3ex]
-9p^2 + 900p - 10179 \ge 0 \\[3ex]
-9(p^2 - 100p + 1131) \ge 0 \\[3ex]
p^2 - 100p + 1131 \le \dfrac{0}{-9} \\[5ex]
p^2 - 100p + 1131 \le 0 \\[3ex]
(p - 13)(p - 87) \le 0 \\[3ex]
Assume:\;\;(p - 13)(p - 87) = 0 \\[3ex]
p - 13 = 0 \;\;\;OR\;\;\; p - 87 = 0 \\[3ex]
p = 13 \;\;\;OR\;\;\; p = 87 \\[3ex]
Test\;\;Intervals\;\;are: \\[3ex]
p \lt 13 \\[3ex]
13 \le p \le 87 \\[3ex]
p \gt 87 \\[3ex]
$
Let:
|
p < 13
p = 0
|
13 ≤ p ≤ 87
p = 17
|
p > 87
p = 87
|
| $p - 13$ |
− |
+ |
+ |
| $p - 87$ |
− |
− |
+ |
| $(p - 13)(p - 87)$ |
+ |
− |
+ |
Less than or equal to zero
means nonnegative
Hence, the second test interval gives the solution of the inequality
The solution is: {
p | 13 ≤ p ≤ 87}
The company should a price between a minimum of
$13.00 and a maximum of
$87.00