(35.) $f(x) = \dfrac{1}{x^2 - x - 6}$
It is a rational function.
First, let us deal with the denominator.
The denominator should not be equal to zero.
The denominator is quadratic. It has two roots.
So, we have to find those two roots.
The denominator should not be equal to those roots
Those roots should not be in our domain because it will give a denominator of zero.
A denominator of zero is an "undefined" function.
$ x^2 - x - 6 \ne 0 \\[3ex] (x + 2)(x - 3) \ne 0 \\[3ex] x + 2 \ne 0 \:\:\:OR\:\:\: x - 3 \ne 0 \\[3ex] x \ne -2 \:\:\:OR\:\:\: x \ne 3 \\[3ex] $ Second, let us deal with the numerator.
The numerator is just $1$. It is a constant.
That is not a problem.
So, our domain will include all real numbers besides $-2$ and $3$
$ D = \{x | x \ne -2, x \ne 3\} \\[3ex] D = (-\infty, -2) \bigcup (-2, 3) \bigcup (3, \infty) \\[3ex] $ To find the range, we have to be "extra careful" here
First, let us assume our output to be $0$
$ y = \dfrac{1}{x^2 - x - 6} \\[5ex] 0 = \dfrac{1}{x^2 - x - 6} \\[5ex] \dfrac{1}{x^2 - x - 6} = 0 \\[5ex] 1 = (x^2 - x - 6) * 0 \\[3ex] 1 = 0? \:This\: is\: a\: contradiction \\[3ex] $ $0$ can never be an output.
Second, let us note that we should only get real numbers as our results.
Consider the fact that the denominator is quadratic.
The discriminant should not be negative because it will lead to complex number results.
So, let us calculate the discriminant.
$ x^2 - x - 6 \\[3ex] Compare:\:\:\: ax^2 + bx + c \\[3ex] a = 1, b = -1, c = -6 \\[3ex] Discriminant = b^2 - 4ac \\[3ex] = (-1)^2 - 4(1)(-6) \\[3ex] = 1 + 24 \\[3ex] = 25 \\[3ex] $ OR
Better still: let us graph it and determine the range from the graph.
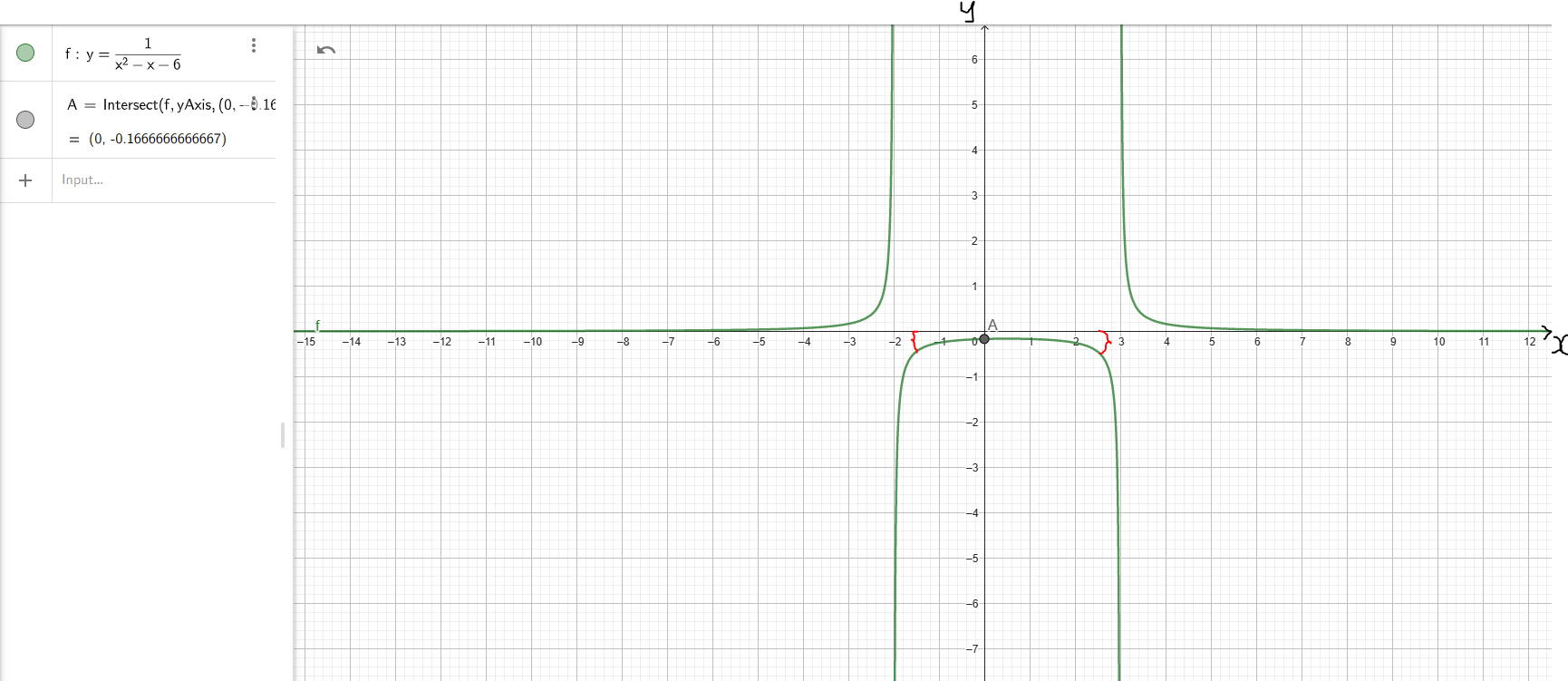
The range will never be zero. It can approach it but can never be it.
The range will never be those y-values in-between the red braces.
It will include everything else.
$ -0.16666666666667 = -\dfrac{4}{25} \\[5ex] R = \{y | y \le -\dfrac{4}{25} \:\:\:OR\:\:\: y \gt 0\} \\[3ex] R = \left(-\infty, -\dfrac{4}{25}\right) \bigcup (0, \infty) $
It is a rational function.
First, let us deal with the denominator.
The denominator should not be equal to zero.
The denominator is quadratic. It has two roots.
So, we have to find those two roots.
The denominator should not be equal to those roots
Those roots should not be in our domain because it will give a denominator of zero.
A denominator of zero is an "undefined" function.
$ x^2 - x - 6 \ne 0 \\[3ex] (x + 2)(x - 3) \ne 0 \\[3ex] x + 2 \ne 0 \:\:\:OR\:\:\: x - 3 \ne 0 \\[3ex] x \ne -2 \:\:\:OR\:\:\: x \ne 3 \\[3ex] $ Second, let us deal with the numerator.
The numerator is just $1$. It is a constant.
That is not a problem.
So, our domain will include all real numbers besides $-2$ and $3$
$ D = \{x | x \ne -2, x \ne 3\} \\[3ex] D = (-\infty, -2) \bigcup (-2, 3) \bigcup (3, \infty) \\[3ex] $ To find the range, we have to be "extra careful" here
First, let us assume our output to be $0$
$ y = \dfrac{1}{x^2 - x - 6} \\[5ex] 0 = \dfrac{1}{x^2 - x - 6} \\[5ex] \dfrac{1}{x^2 - x - 6} = 0 \\[5ex] 1 = (x^2 - x - 6) * 0 \\[3ex] 1 = 0? \:This\: is\: a\: contradiction \\[3ex] $ $0$ can never be an output.
Second, let us note that we should only get real numbers as our results.
Consider the fact that the denominator is quadratic.
The discriminant should not be negative because it will lead to complex number results.
So, let us calculate the discriminant.
$ x^2 - x - 6 \\[3ex] Compare:\:\:\: ax^2 + bx + c \\[3ex] a = 1, b = -1, c = -6 \\[3ex] Discriminant = b^2 - 4ac \\[3ex] = (-1)^2 - 4(1)(-6) \\[3ex] = 1 + 24 \\[3ex] = 25 \\[3ex] $ OR
Better still: let us graph it and determine the range from the graph.

The range will never be zero. It can approach it but can never be it.
The range will never be those y-values in-between the red braces.
It will include everything else.
$ -0.16666666666667 = -\dfrac{4}{25} \\[5ex] R = \{y | y \le -\dfrac{4}{25} \:\:\:OR\:\:\: y \gt 0\} \\[3ex] R = \left(-\infty, -\dfrac{4}{25}\right) \bigcup (0, \infty) $
(36.) $f(x) = \sqrt{3 - 5x}$
It is a function (positive square root function).
It is also a one-to-one function.
Each input has an exactly one output.
To find the domain, the radicand (the value inside the square root radical) must not be negative.
Square root of negative numbers are not real numbers. They are imaginary numbers.
We are only dealing with real numbers.
So, the radicand must be a nonnegative number (zero and positive number).
That means that the radicand must be at least zero.
$ 3 - 5x \ge 0 \\[3ex] 3 - 0 \ge 5x \\[3ex] 3 \ge 5x \\[3ex] 5x \le 3 \\[3ex] x \le \dfrac{3}{5} \\[5ex] D = \{x : x \le \dfrac{3}{5}\} \\[5ex] D = \left(-\infty, \dfrac{3}{5}\right] \\[5ex] $ For the range, there is only the plus sign in front of the radical.
The smallest "real number" output value occurs for the smallest input value.
The smallest input value is $\dfrac{3}{5}$
$ 3 - 5x \\[3ex] 3 - 5 * \dfrac{3}{5} \\[5ex] 3 - 3 \\[3ex] 0 \\[3ex] \sqrt{0} = 0 \\[3ex] $ The smallest output value is $0$
The range can only include nonnegative numbers (zero and positive numbers).
$ R = \{y | y \ge 0\} \\[3ex] R = [0, \infty) $
It is a function (positive square root function).
It is also a one-to-one function.
Each input has an exactly one output.
To find the domain, the radicand (the value inside the square root radical) must not be negative.
Square root of negative numbers are not real numbers. They are imaginary numbers.
We are only dealing with real numbers.
So, the radicand must be a nonnegative number (zero and positive number).
That means that the radicand must be at least zero.
$ 3 - 5x \ge 0 \\[3ex] 3 - 0 \ge 5x \\[3ex] 3 \ge 5x \\[3ex] 5x \le 3 \\[3ex] x \le \dfrac{3}{5} \\[5ex] D = \{x : x \le \dfrac{3}{5}\} \\[5ex] D = \left(-\infty, \dfrac{3}{5}\right] \\[5ex] $ For the range, there is only the plus sign in front of the radical.
The smallest "real number" output value occurs for the smallest input value.
The smallest input value is $\dfrac{3}{5}$
$ 3 - 5x \\[3ex] 3 - 5 * \dfrac{3}{5} \\[5ex] 3 - 3 \\[3ex] 0 \\[3ex] \sqrt{0} = 0 \\[3ex] $ The smallest output value is $0$
The range can only include nonnegative numbers (zero and positive numbers).
$ R = \{y | y \ge 0\} \\[3ex] R = [0, \infty) $