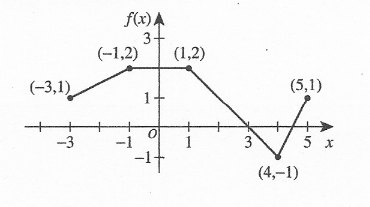
(15.) ACT The function $f(x)$ is shown below with several points labeled.
Another function, $g(x)$ is defined such that $g(x) = -[f(x) - 3]$.
What is $g(4)$?
 $
F.\:\: -4 \\[3ex]
G.\:\: -1 \\[3ex]
H.\:\: 1 \\[3ex]
J.\:\: 4 \\[3ex]
K.\:\: 7 \\[3ex]
$
$
F.\:\: -4 \\[3ex]
G.\:\: -1 \\[3ex]
H.\:\: 1 \\[3ex]
J.\:\: 4 \\[3ex]
K.\:\: 7 \\[3ex]
$
$ g(x) = -[f(x) - 3] \\[3ex] For\:\:g(4),\:\:x = 4 \\[3ex] g(4) = -[f(4) - 3] \\[3ex] f(4) = -1 \\[3ex] \implies \\[3ex] g(4) = -[-1 - 3] \\[3ex] g(4) = -(-4) \\[3ex] g(4) = 4 $
Another function, $g(x)$ is defined such that $g(x) = -[f(x) - 3]$.
What is $g(4)$?

$ g(x) = -[f(x) - 3] \\[3ex] For\:\:g(4),\:\:x = 4 \\[3ex] g(4) = -[f(4) - 3] \\[3ex] f(4) = -1 \\[3ex] \implies \\[3ex] g(4) = -[-1 - 3] \\[3ex] g(4) = -(-4) \\[3ex] g(4) = 4 $
(16.) ACT Let a function of $2$ variables be defined by $f(x, y) = xy - (x - y)$.
What is the value of $f(10, 3)$?
$f(10, 3)$
This means that we have to substitute $10$ for $x$ and $3$ for $y$
$ f(x, y) = xy - (x - y) \\[3ex] f(10, 3) = 10(3) - (10 - 3) \\[3ex] f(10, 3) = 30 - 7 \\[3ex] f(10, 3) = 23 $
What is the value of $f(10, 3)$?
$f(10, 3)$
This means that we have to substitute $10$ for $x$ and $3$ for $y$
$ f(x, y) = xy - (x - y) \\[3ex] f(10, 3) = 10(3) - (10 - 3) \\[3ex] f(10, 3) = 30 - 7 \\[3ex] f(10, 3) = 23 $