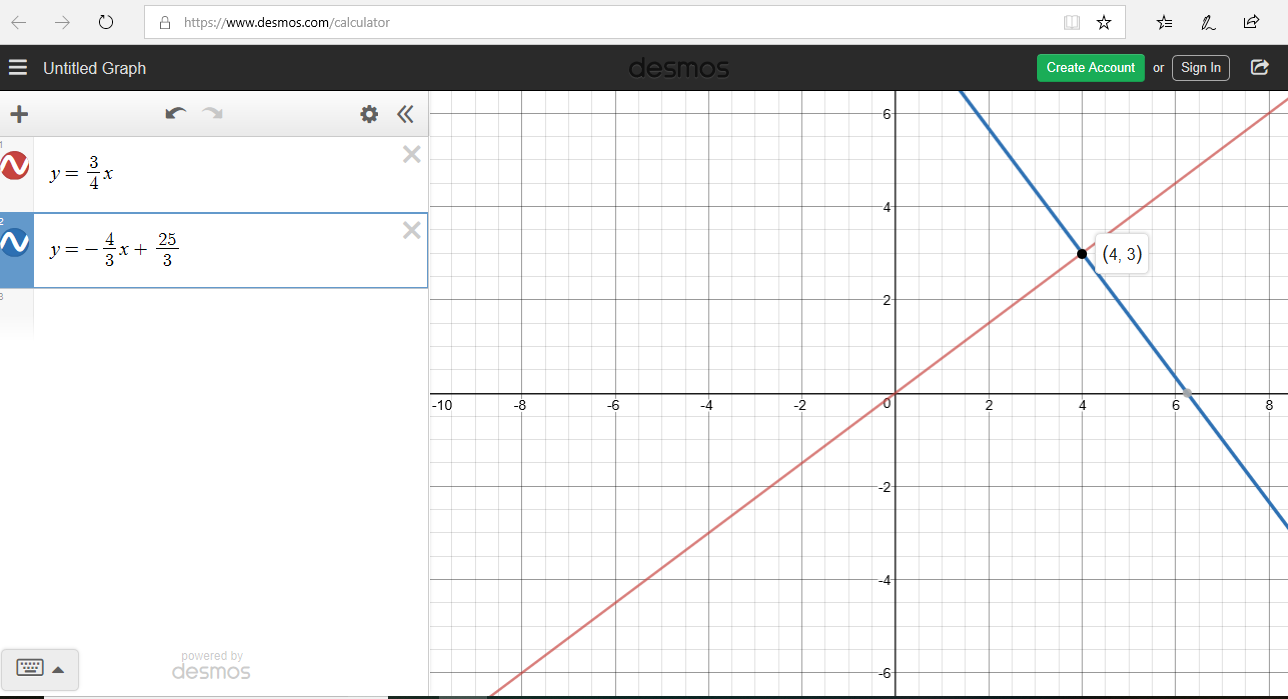
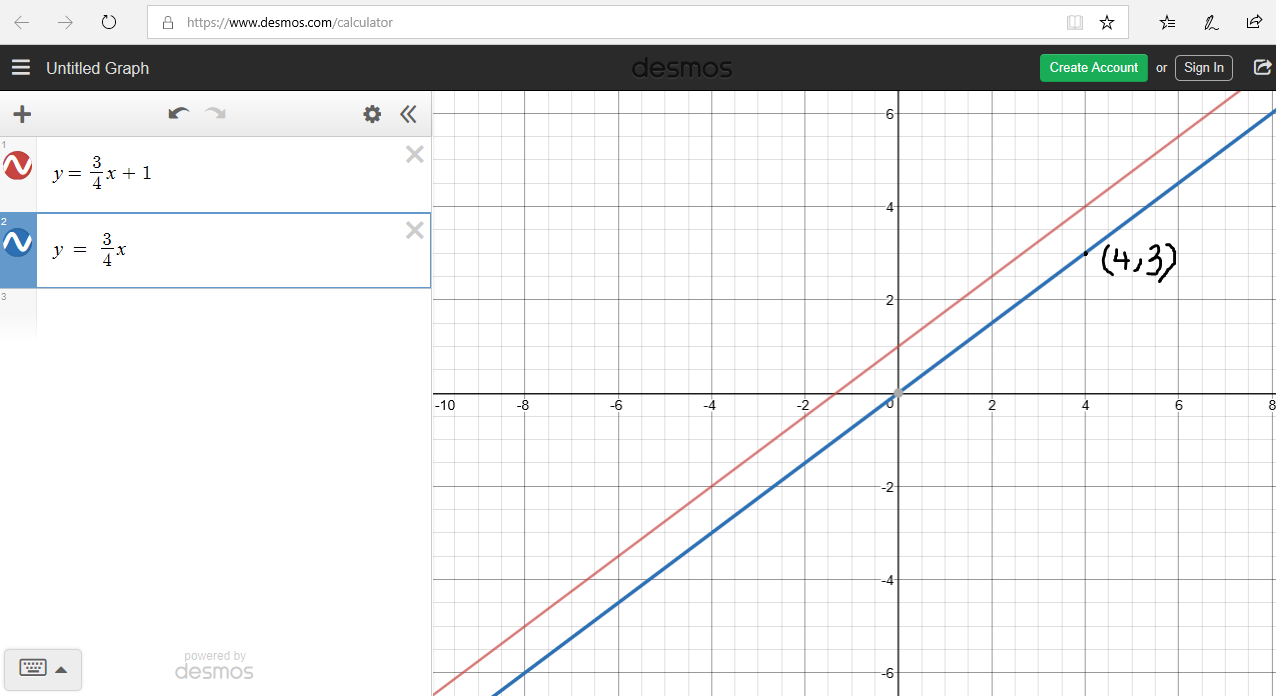
(17.) Determine the equation of a line that is parallel to $y = \dfrac{3}{4}x + 1$
and passes through $(4, 3)$.
Write your answer in slope-intercept form and standard form.
Two lines are parallel to each other if their slopes are the same
$\underline{Line\:\: 1}$
$y = \dfrac{3}{4}x + 1$
Slope of Line $1$ = $m_1$
$m_1 = \dfrac{3}{4}$
$\underline{Line\:\: 2}$
$Line\:\: 2 \parallel Line\:\: 1$
Slope of Line $2$ = $m_2$
$ m_2 = \dfrac{3}{4} \\[5ex] $ ${Line\:\: 2}$ should pass through the point $(4, 3)$
To find ${Line\:\: 2}$, we shall use the Point-Slope form because we have a slope and a point
Point-Slope Form: $y - y_1 = m(x - x_1)$
$ m_2 = \dfrac{3}{4} \\[5ex] x_1 = 4, y_1 = 3 \\[3ex] y - y_1 = m(x - x_1) \\[3ex] y - 3 = \dfrac{3}{4}(x - 4) \\[5ex] y = \dfrac{3}{4}(x - 4) + 3 \\[5ex] y = \dfrac{3}{4}x - 3 + 3 \\[5ex] y = \dfrac{3}{4}x \\[5ex] $ The equation of ${Line\:\: 2}$ in Slope-Intercept form is: $y = \dfrac{3}{4}x$
To write ${Line\:\: 2}$ in Standard form;
Multiply each term by the $LCD$
$LCD = 4$
$ 4 * y = 4 * \dfrac{3}{4}x \\[5ex] 4y = 3x \\[3ex] 3x = 4y \\[3ex] 3x - 4y = 0 \\[3ex] $ The equation of ${Line\:\: 2}$ in Standard form is: $3x - 4y = 0$
and passes through $(4, 3)$.
Write your answer in slope-intercept form and standard form.
Two lines are parallel to each other if their slopes are the same
$\underline{Line\:\: 1}$
$y = \dfrac{3}{4}x + 1$
Slope of Line $1$ = $m_1$
$m_1 = \dfrac{3}{4}$
$\underline{Line\:\: 2}$
$Line\:\: 2 \parallel Line\:\: 1$
Slope of Line $2$ = $m_2$
$ m_2 = \dfrac{3}{4} \\[5ex] $ ${Line\:\: 2}$ should pass through the point $(4, 3)$
To find ${Line\:\: 2}$, we shall use the Point-Slope form because we have a slope and a point
Point-Slope Form: $y - y_1 = m(x - x_1)$
$ m_2 = \dfrac{3}{4} \\[5ex] x_1 = 4, y_1 = 3 \\[3ex] y - y_1 = m(x - x_1) \\[3ex] y - 3 = \dfrac{3}{4}(x - 4) \\[5ex] y = \dfrac{3}{4}(x - 4) + 3 \\[5ex] y = \dfrac{3}{4}x - 3 + 3 \\[5ex] y = \dfrac{3}{4}x \\[5ex] $ The equation of ${Line\:\: 2}$ in Slope-Intercept form is: $y = \dfrac{3}{4}x$
To write ${Line\:\: 2}$ in Standard form;
Multiply each term by the $LCD$
$LCD = 4$
$ 4 * y = 4 * \dfrac{3}{4}x \\[5ex] 4y = 3x \\[3ex] 3x = 4y \\[3ex] 3x - 4y = 0 \\[3ex] $ The equation of ${Line\:\: 2}$ in Standard form is: $3x - 4y = 0$

(18.) Determine the value of $p$ so that the line containing the points $(-3, p)$ and
$(4, 8)$
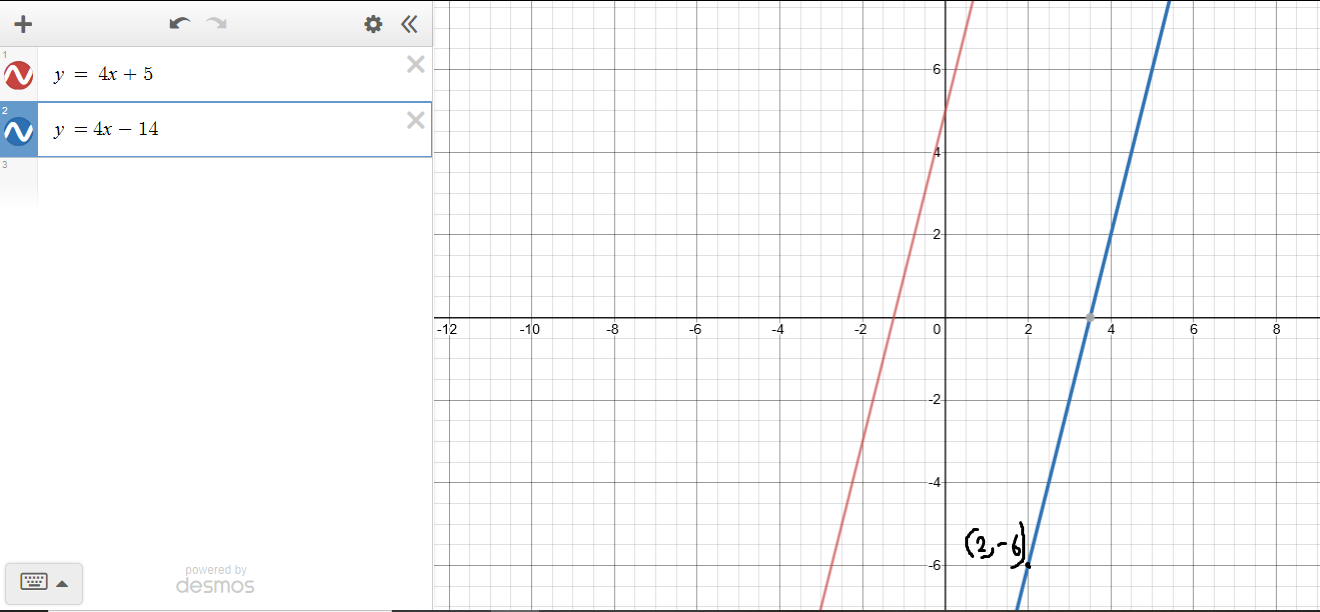
is parallel to the line containing the points $(7, 3)$ and $(3, -6)$
Two lines are parallel to each other if their slopes are the same
$\underline{Line\:\: 1}$
Slope of Line $1$ = $m_1$
Point $1$ is $(-3, p)$
$x_1 = -3$
$y_1 = p$
Point $2$ is $(4, 8)$
$x_2 = 4$
$y_2 = 8$
$ m_1 = \dfrac{y_2 - y_1}{x_2 - x_1} \\[5ex] m_1 = \dfrac{8 - p}{4 - (-3)} \\[5ex] m_1 = \dfrac{8 - p}{4 + 3} \\[5ex] m_1 = \dfrac{8 - p}{7} \\[5ex] $ $\underline{Line\:\: 2}$
Slope of Line $1$ = $m_2$
Point $1$ is $(7, 3)$
$x_1 = 7$
$y_1 = 3$
Point $2$ is $(3, -6)$
$x_2 = 3$
$y_2 = -6$
$ m_2 = \dfrac{y_2 - y_1}{x_2 - x_1} \\[5ex] m_2 = \dfrac{-6 - 3}{3 - 7} \\[5ex] m_2 = \dfrac{-9}{-4} \\[5ex] m_2 = \dfrac{9}{4} \\[5ex] $ $Line\:\: 1 \parallel Line\:\: 2$
$ m_1 = m_2 \\[3ex] \dfrac{8 - p}{7} = \dfrac{9}{4} \\[5ex] $ Multiply each term by the $LCD$
$LCD = 28$
$ 28 * \dfrac{8 - p}{7} = 28 * \dfrac{9}{4} \\[5ex] 4(8 - p) = 7(9) \\[3ex] 4(8) - 4(p) = 63 \\[3ex] 32 - 4p = 63 \\[3ex] 32 - 63 = 4p \\[3ex] -31 = 4p \\[3ex] 4p = -31 \\[3ex] p = -\dfrac{31}{4} $
is parallel to the line containing the points $(7, 3)$ and $(3, -6)$
Two lines are parallel to each other if their slopes are the same
$\underline{Line\:\: 1}$
Slope of Line $1$ = $m_1$
Point $1$ is $(-3, p)$
$x_1 = -3$
$y_1 = p$
Point $2$ is $(4, 8)$
$x_2 = 4$
$y_2 = 8$
$ m_1 = \dfrac{y_2 - y_1}{x_2 - x_1} \\[5ex] m_1 = \dfrac{8 - p}{4 - (-3)} \\[5ex] m_1 = \dfrac{8 - p}{4 + 3} \\[5ex] m_1 = \dfrac{8 - p}{7} \\[5ex] $ $\underline{Line\:\: 2}$
Slope of Line $1$ = $m_2$
Point $1$ is $(7, 3)$
$x_1 = 7$
$y_1 = 3$
Point $2$ is $(3, -6)$
$x_2 = 3$
$y_2 = -6$
$ m_2 = \dfrac{y_2 - y_1}{x_2 - x_1} \\[5ex] m_2 = \dfrac{-6 - 3}{3 - 7} \\[5ex] m_2 = \dfrac{-9}{-4} \\[5ex] m_2 = \dfrac{9}{4} \\[5ex] $ $Line\:\: 1 \parallel Line\:\: 2$
$ m_1 = m_2 \\[3ex] \dfrac{8 - p}{7} = \dfrac{9}{4} \\[5ex] $ Multiply each term by the $LCD$
$LCD = 28$
$ 28 * \dfrac{8 - p}{7} = 28 * \dfrac{9}{4} \\[5ex] 4(8 - p) = 7(9) \\[3ex] 4(8) - 4(p) = 63 \\[3ex] 32 - 4p = 63 \\[3ex] 32 - 63 = 4p \\[3ex] -31 = 4p \\[3ex] 4p = -31 \\[3ex] p = -\dfrac{31}{4} $