(5.) ACT Shasta is participating in a bike ride for charity.
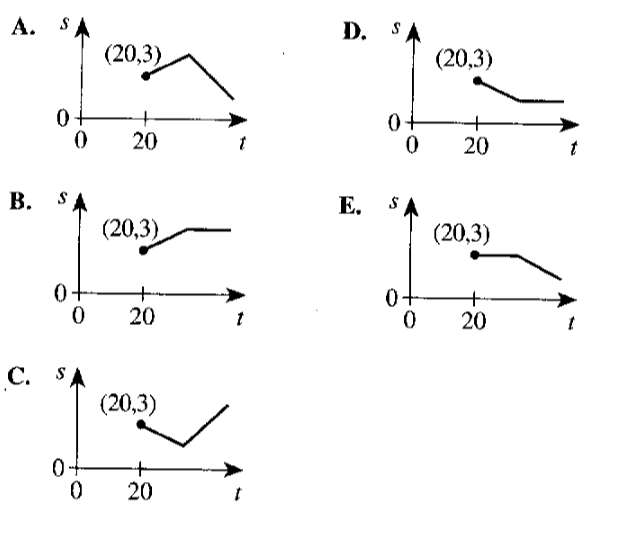
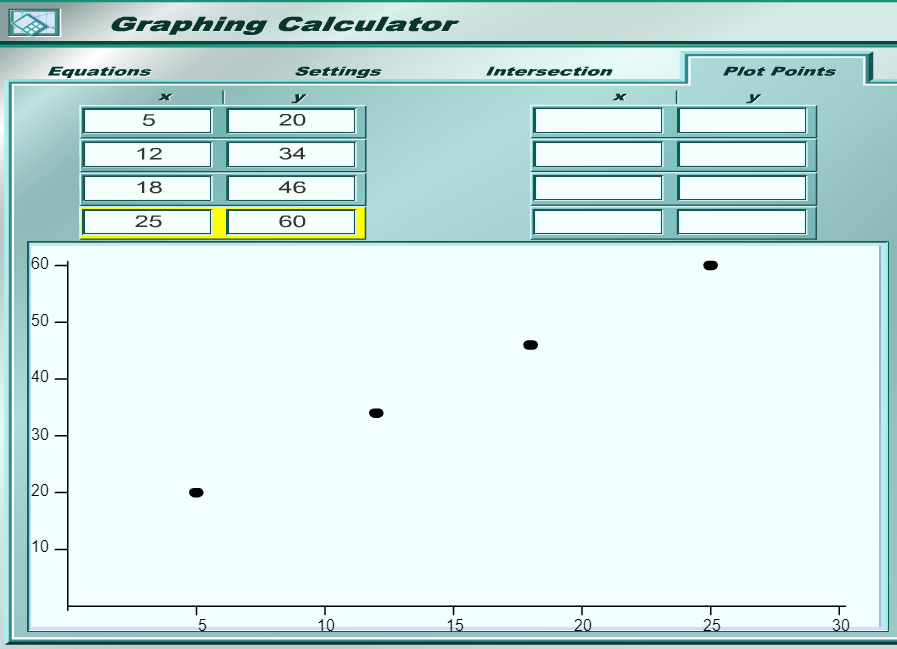
The graph of speed $(s)$ versus time $(t)$ for the first $20$ seconds of her bike ride is shown in the coordinate plane below.
The graph is composed of $2$ line segments for which the endpoints are at $(0, 0), (10, 5),$ and $(20, 3)$.
Shasta traveled $25$ meters in the first $10$ seconds.
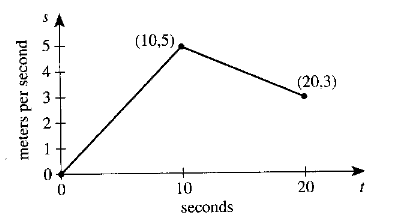
Beginning at $t = 20$ seconds, Shasta slows down as she approaches a familiar group of riders ahead of her and then travels at a constant speed with the group after joining them.
What is Shasta's speed, in meters per second, at $t = 3$ seconds?
$ F.\:\: 1.5 \\[3ex] G.\:\: 2.0 \\[3ex] H.\:\: 2.5 \\[3ex] J.\:\: 3.0 \\[3ex] K.\:\: 6.0 \\[3ex] $
The first $3$ seconds lies in the first line segment whose endpoints are $(0, 0)$ and $(10, 5)$
First: We need to find the slope
Second: We have to write the equation of the line joining those points in Slope-Intercept form
$ Point\:\:1 = (0, 0) \\[3ex] x_1 = 0 \\[3ex] y_1 = 0 \\[3ex] y-intercept, b = 0 \\[3ex] Point\:2 = (10, 5) \\[3ex] x_2 = 10 \\[3ex] y_2 = 5 \\[3ex] Slope, m = \dfrac{y_2 - y_1}{x_2 - x_1} \\[5ex] m = \dfrac{5 - 0}{10 - 0} \\[5ex] m = \dfrac{5}{10} \\[5ex] m = \dfrac{1}{2} \\[5ex] y = mx + b \\[3ex] y = \dfrac{1}{2}x + 0 \\[5ex] y = \dfrac{1}{2}x \\[3ex] This\:\:implies\:\:that \\[3ex] s = \dfrac{1}{2}t \\[5ex] when\:\:t = 3 \\[3ex] s = \dfrac{1}{2} * 3 \\[5ex] s = \dfrac{3}{2} \\[5ex] s = 1.5\:ms^{-1} $
The graph of speed $(s)$ versus time $(t)$ for the first $20$ seconds of her bike ride is shown in the coordinate plane below.
The graph is composed of $2$ line segments for which the endpoints are at $(0, 0), (10, 5),$ and $(20, 3)$.
Shasta traveled $25$ meters in the first $10$ seconds.

Beginning at $t = 20$ seconds, Shasta slows down as she approaches a familiar group of riders ahead of her and then travels at a constant speed with the group after joining them.
What is Shasta's speed, in meters per second, at $t = 3$ seconds?
$ F.\:\: 1.5 \\[3ex] G.\:\: 2.0 \\[3ex] H.\:\: 2.5 \\[3ex] J.\:\: 3.0 \\[3ex] K.\:\: 6.0 \\[3ex] $
The first $3$ seconds lies in the first line segment whose endpoints are $(0, 0)$ and $(10, 5)$
First: We need to find the slope
Second: We have to write the equation of the line joining those points in Slope-Intercept form
$ Point\:\:1 = (0, 0) \\[3ex] x_1 = 0 \\[3ex] y_1 = 0 \\[3ex] y-intercept, b = 0 \\[3ex] Point\:2 = (10, 5) \\[3ex] x_2 = 10 \\[3ex] y_2 = 5 \\[3ex] Slope, m = \dfrac{y_2 - y_1}{x_2 - x_1} \\[5ex] m = \dfrac{5 - 0}{10 - 0} \\[5ex] m = \dfrac{5}{10} \\[5ex] m = \dfrac{1}{2} \\[5ex] y = mx + b \\[3ex] y = \dfrac{1}{2}x + 0 \\[5ex] y = \dfrac{1}{2}x \\[3ex] This\:\:implies\:\:that \\[3ex] s = \dfrac{1}{2}t \\[5ex] when\:\:t = 3 \\[3ex] s = \dfrac{1}{2} * 3 \\[5ex] s = \dfrac{3}{2} \\[5ex] s = 1.5\:ms^{-1} $
(6.) ACT Based on Question $5$
Shasta's acceleration, $a$, over the interval from $t = 10$ seconds to $t = 20$ seconds, is equal to the slope of the graph over that interval, measured in meters per second per second.
What is the value of $a$?
$ A.\:\: -5 \\[3ex] B.\:\: -\dfrac{1}{5} \\[5ex] C.\:\: \dfrac{1}{5} \\[5ex] D.\:\: 2 \\[3ex] E.\:\: 5 \\[3ex] $
$ Point\:\:1 = (10, 5) \\[3ex] x_1 = 10 \\[3ex] y_1 = 5 \\[3ex] Point\:2 = (20, 3) \\[3ex] x_2 = 20 \\[3ex] y_2 = 3 \\[3ex] Slope, m = \dfrac{y_2 - y_1}{x_2 - x_1} \\[5ex] m = \dfrac{3 - 5}{20 - 10} \\[5ex] m = \dfrac{-2}{10} \\[5ex] m = \dfrac{-1}{5} \\[5ex] a = m \\[3ex] \therefore a = -\dfrac{1}{5}\:ms^{-2} $
Shasta's acceleration, $a$, over the interval from $t = 10$ seconds to $t = 20$ seconds, is equal to the slope of the graph over that interval, measured in meters per second per second.
What is the value of $a$?
$ A.\:\: -5 \\[3ex] B.\:\: -\dfrac{1}{5} \\[5ex] C.\:\: \dfrac{1}{5} \\[5ex] D.\:\: 2 \\[3ex] E.\:\: 5 \\[3ex] $
$ Point\:\:1 = (10, 5) \\[3ex] x_1 = 10 \\[3ex] y_1 = 5 \\[3ex] Point\:2 = (20, 3) \\[3ex] x_2 = 20 \\[3ex] y_2 = 3 \\[3ex] Slope, m = \dfrac{y_2 - y_1}{x_2 - x_1} \\[5ex] m = \dfrac{3 - 5}{20 - 10} \\[5ex] m = \dfrac{-2}{10} \\[5ex] m = \dfrac{-1}{5} \\[5ex] a = m \\[3ex] \therefore a = -\dfrac{1}{5}\:ms^{-2} $