Solved Examples on Linear Models
Attempt all questions.
Show all work.
(1.) Examine these scatter plots and determine whether each relation is linear or nonlinear.
(a.)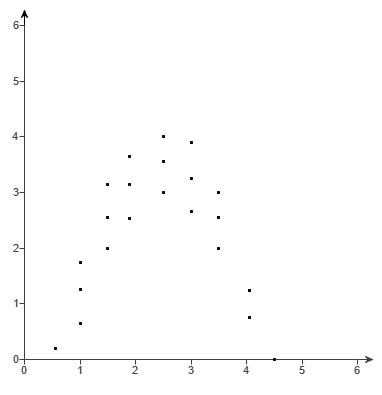
(b.)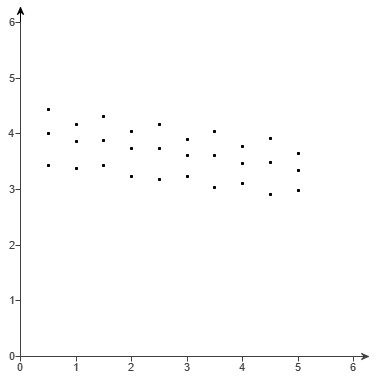
(c.)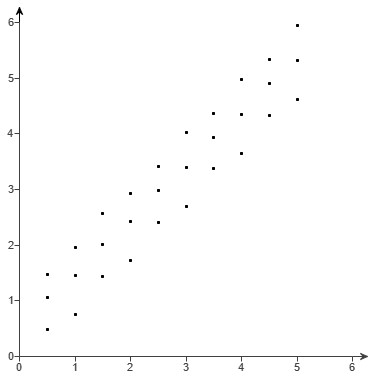
(d.)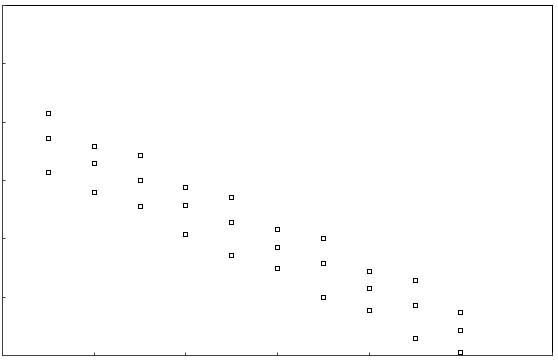
(e.)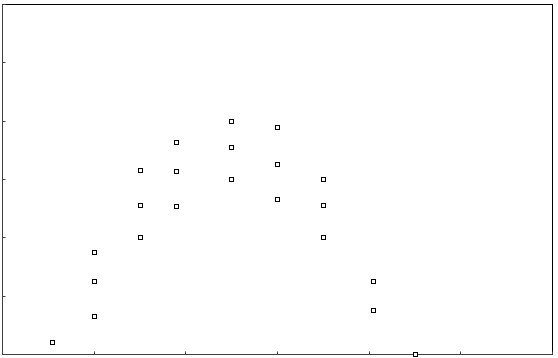
(f.)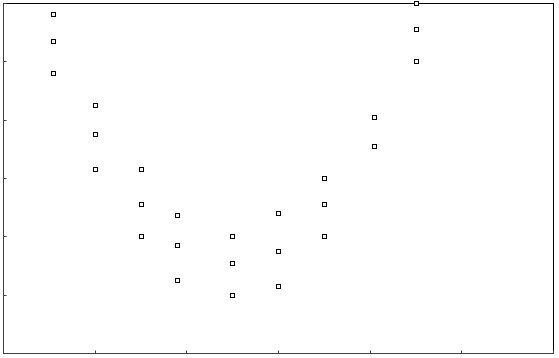
(a.) The relation is nonlinear because the data points in the scatter plot does not follow the pattern of a straight line.
It follows the pattern of the curve of a quadratic model: concave down.
(b.) The relation is linear because the data points in the scatter plot follow the pattern of a straight line.
The straight line pattern is that of a negative slope.
(c.) The relation is linear because the data points in the scatter plot follow the pattern of a straight line.
The straight line pattern is that of a positive slope.
(d.) The relation is linear because the data points in the scatter plot follow the pattern of a straight line.
The straight line pattern is that of a negative slope.
(e.) The relation is nonlinear because the data points in the scatter plot does not follow the pattern of a straight line.
It follows the pattern of the curve of a quadratic model: concave down.
(f.) The relation is nonlinear because the data points in the scatter plot does not follow the pattern of a straight line.
It follows the pattern of the curve of a quadratic model: concave up.
(a.)

(b.)

(c.)

(d.)

(e.)

(f.)

(a.) The relation is nonlinear because the data points in the scatter plot does not follow the pattern of a straight line.
It follows the pattern of the curve of a quadratic model: concave down.
(b.) The relation is linear because the data points in the scatter plot follow the pattern of a straight line.
The straight line pattern is that of a negative slope.
(c.) The relation is linear because the data points in the scatter plot follow the pattern of a straight line.
The straight line pattern is that of a positive slope.
(d.) The relation is linear because the data points in the scatter plot follow the pattern of a straight line.
The straight line pattern is that of a negative slope.
(e.) The relation is nonlinear because the data points in the scatter plot does not follow the pattern of a straight line.
It follows the pattern of the curve of a quadratic model: concave down.
(f.) The relation is nonlinear because the data points in the scatter plot does not follow the pattern of a straight line.
It follows the pattern of the curve of a quadratic model: concave up.
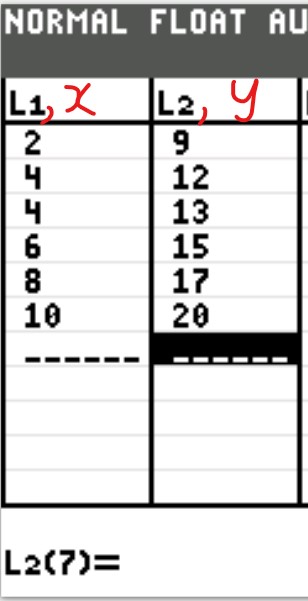
(2.) For the data given below:
(a.) Draw a scatter plot.
[Please see the use of Texas Instruments calculators to draw the scatter plot. Answer: (2.)(a.)]
(b.) Find the equation of the line containing the first and last data points.
(c.) Graph the line found in part (b.) on the scatter plot.
[Please see the use of Texas Instruments calculators to graph the line on the scatter plot. Answer: (2.)(c.)]
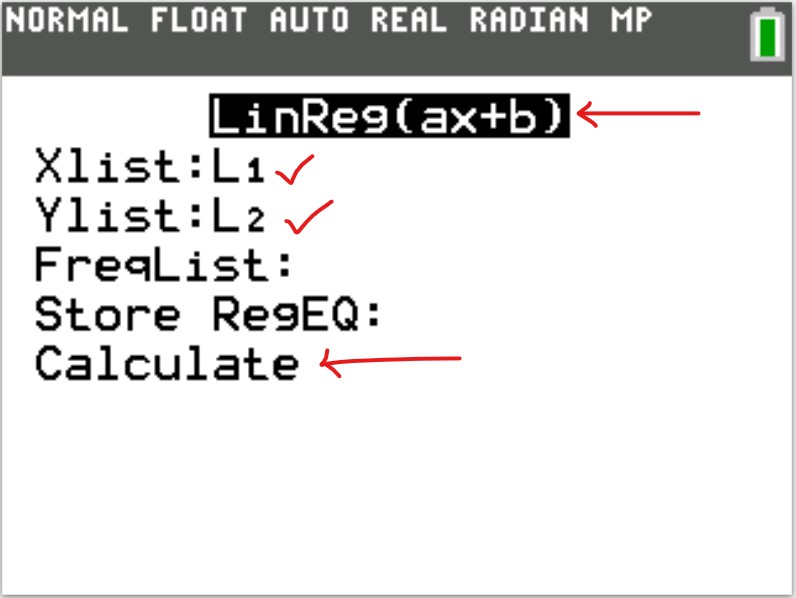
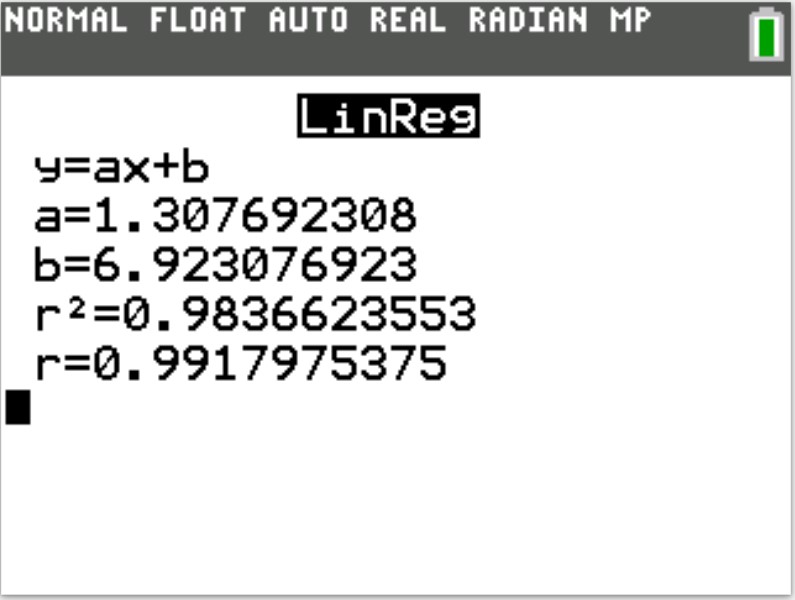
(d.) Use a graphing utility to find the line of best fit.
Type integers or decimals rounded to four decimal places as needed.
[Please see the use of Texas Instruments calculators to determine the regression equation (also known as the line of best fit). Answer: (2.)(d.)]
(e.) What is the correlation coefficient, r?
Type an integer or decimal rounded to three decimal places as needed.
[Please see the use of Texas Instruments calculators to determine the correlation coefficient. Answer: (2.)(e.)]
(f.) Use a graphing utility to draw the scatter plot and graph the line of best fit on it using these values:
Xmin = 0, Xmax = 20, Xscl = 2, Ymin= 0, Ymax = 20, Yscl = 2
[Please see the use of Texas Instruments calculators to draw the scatter plot and the line of best fit. Answer: (2.)(f.)]
(a.) Please see the use of Texas Instruments calculators to draw the scatter plot. Answer: (2.)(a.)
$ (b.) \\[3ex] First\;\;Point = (3, 3) \\[3ex] x_1 = 3 \\[3ex] y_1 = 3 \\[3ex] Last\;\;Point = (9, 15) \\[3ex] x_2 = 9 \\[3ex] y_2 = 15 \\[3ex] slope = m = \dfrac{y_2 - y_1}{x_2 - x_1} \\[5ex] = \dfrac{15 - 3}{9 - 3} \\[5ex] = \dfrac{12}{6} \\[5ex] = 2 \\[3ex] To\;\;find\;\;the\;\;y-intercept: \\[3ex] Use\;\;any\;\;point \\[3ex] Let\;\;us\;\;use\;\;Last\;\;Point = (9, 15) \\[3ex] x = 9 \\[3ex] y = 15 \\[3ex] y = mx + b \\[3ex] 15 = 2(9) + b \\[3ex] 15 = 18 + b \\[3ex] 18 + b = 15 \\[3ex] b = 15 - 18 \\[3ex] b = -3 \\[3ex] \implies \\[3ex] y = mx + b \\[3ex] y = 2x - 3 \\[3ex] $ (c.) Please see the use of Texas Instruments calculators to graph the line on the scatter plot: Answer: (2.)(c.)
(d.) Please see the use of Texas Instruments calculators to determine the line of best fit (also known as the least-squares regression line): Answer: (2.)(d.)
(e.) Please see the use of Texas Instruments calculators to determine the correlation coefficient: Answer: (2.)(e.)
(f.) Please see the use of Texas Instruments calculators to draw the scatter plot and graph the line of best fit using those settings: Answer: (2.)(f.)
| x | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| y | 3 | 5 | 6 | 9 | 11 | 13 | 15 |
(a.) Draw a scatter plot.
[Please see the use of Texas Instruments calculators to draw the scatter plot. Answer: (2.)(a.)]
(b.) Find the equation of the line containing the first and last data points.
(c.) Graph the line found in part (b.) on the scatter plot.
[Please see the use of Texas Instruments calculators to graph the line on the scatter plot. Answer: (2.)(c.)]
(d.) Use a graphing utility to find the line of best fit.
Type integers or decimals rounded to four decimal places as needed.
[Please see the use of Texas Instruments calculators to determine the regression equation (also known as the line of best fit). Answer: (2.)(d.)]
(e.) What is the correlation coefficient, r?
Type an integer or decimal rounded to three decimal places as needed.
[Please see the use of Texas Instruments calculators to determine the correlation coefficient. Answer: (2.)(e.)]
(f.) Use a graphing utility to draw the scatter plot and graph the line of best fit on it using these values:
Xmin = 0, Xmax = 20, Xscl = 2, Ymin= 0, Ymax = 20, Yscl = 2
[Please see the use of Texas Instruments calculators to draw the scatter plot and the line of best fit. Answer: (2.)(f.)]
(a.) Please see the use of Texas Instruments calculators to draw the scatter plot. Answer: (2.)(a.)
$ (b.) \\[3ex] First\;\;Point = (3, 3) \\[3ex] x_1 = 3 \\[3ex] y_1 = 3 \\[3ex] Last\;\;Point = (9, 15) \\[3ex] x_2 = 9 \\[3ex] y_2 = 15 \\[3ex] slope = m = \dfrac{y_2 - y_1}{x_2 - x_1} \\[5ex] = \dfrac{15 - 3}{9 - 3} \\[5ex] = \dfrac{12}{6} \\[5ex] = 2 \\[3ex] To\;\;find\;\;the\;\;y-intercept: \\[3ex] Use\;\;any\;\;point \\[3ex] Let\;\;us\;\;use\;\;Last\;\;Point = (9, 15) \\[3ex] x = 9 \\[3ex] y = 15 \\[3ex] y = mx + b \\[3ex] 15 = 2(9) + b \\[3ex] 15 = 18 + b \\[3ex] 18 + b = 15 \\[3ex] b = 15 - 18 \\[3ex] b = -3 \\[3ex] \implies \\[3ex] y = mx + b \\[3ex] y = 2x - 3 \\[3ex] $ (c.) Please see the use of Texas Instruments calculators to graph the line on the scatter plot: Answer: (2.)(c.)
(d.) Please see the use of Texas Instruments calculators to determine the line of best fit (also known as the least-squares regression line): Answer: (2.)(d.)
(e.) Please see the use of Texas Instruments calculators to determine the correlation coefficient: Answer: (2.)(e.)
(f.) Please see the use of Texas Instruments calculators to draw the scatter plot and graph the line of best fit using those settings: Answer: (2.)(f.)