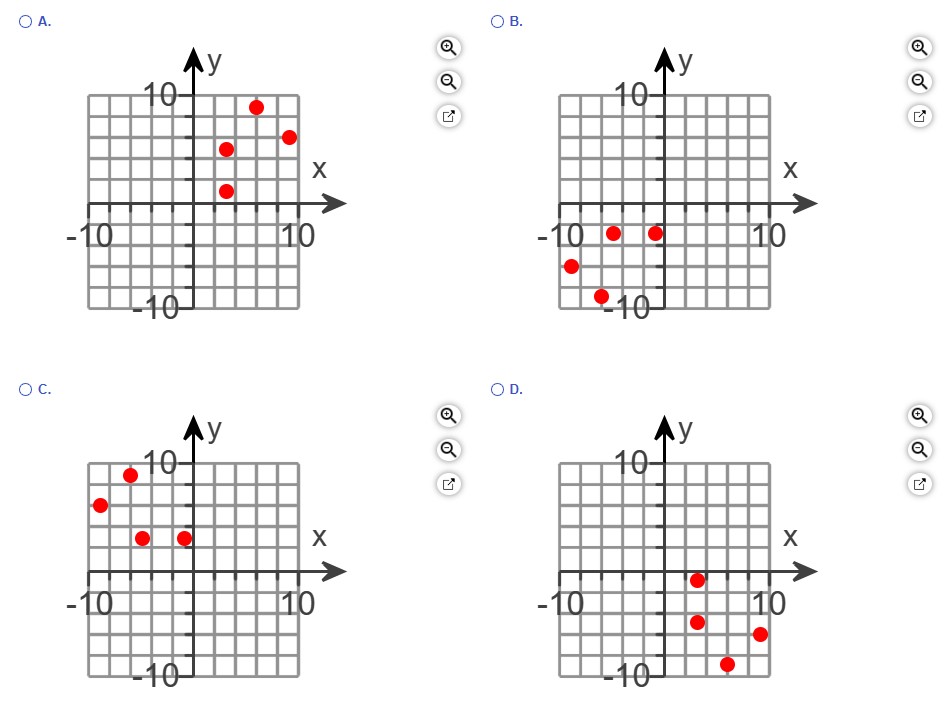
(3.) (a.) Plot the points (3, −1), (6, −9), (9, −6), (3, −5) in the Cartesian plane.
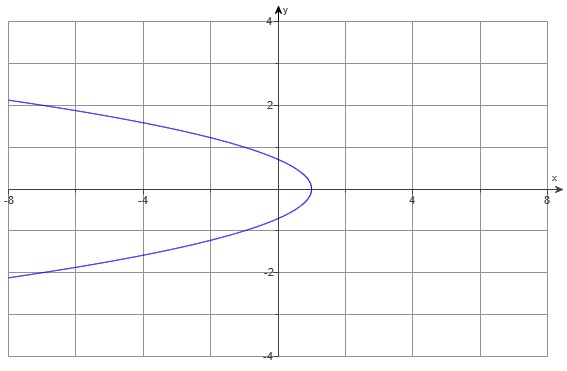
Choose the correct graph.
(b.) Does the relation represent a function? Why?
A. Yes, because there are ordered pairs with the same first element and different second elements.
B. Yes, because there are no ordered pairs with the same first element and different second elements.
C. No, because there are no ordered pairs with the same first element and different second elements.
D. No, because there are ordered pairs with the same first element and different second elements.
(a.) Scale: 1 cm represents 2 units (Not drawn to scale)
The correct graph representing the points is Option D.:
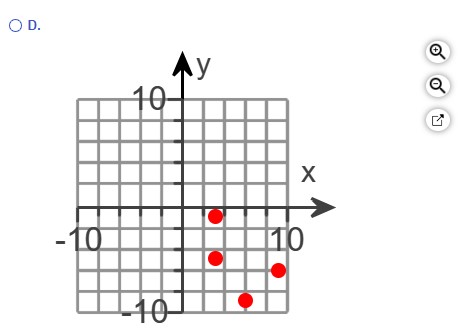
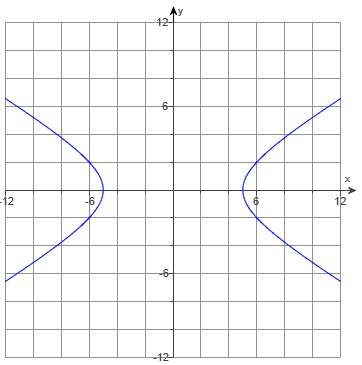
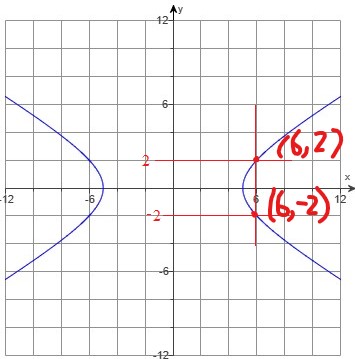
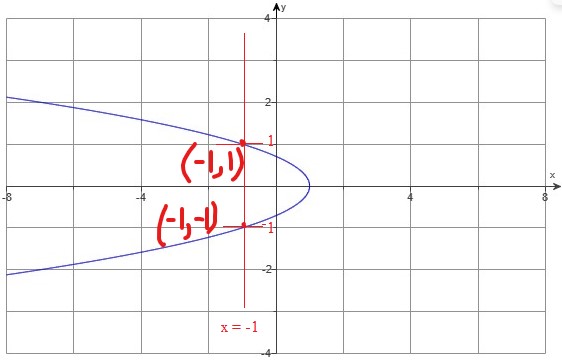
(b.) The relation is not a function because there is an input, 3 that has two different outputs, −1 and −5
D. No, because there are ordered pairs with the same first element and different second elements.
Choose the correct graph.

(b.) Does the relation represent a function? Why?
A. Yes, because there are ordered pairs with the same first element and different second elements.
B. Yes, because there are no ordered pairs with the same first element and different second elements.
C. No, because there are no ordered pairs with the same first element and different second elements.
D. No, because there are ordered pairs with the same first element and different second elements.
(a.) Scale: 1 cm represents 2 units (Not drawn to scale)
The correct graph representing the points is Option D.:

(b.) The relation is not a function because there is an input, 3 that has two different outputs, −1 and −5
D. No, because there are ordered pairs with the same first element and different second elements.
(4.)