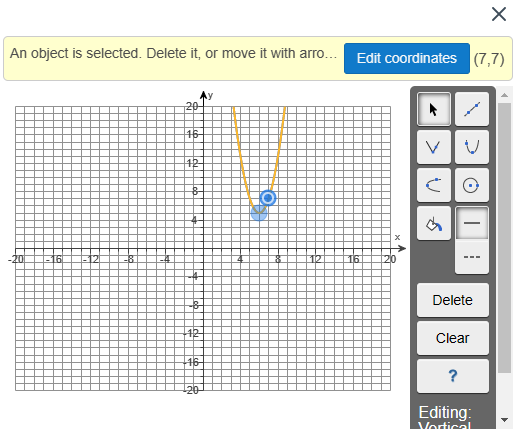
(3.) For the quadratic function: $f(x) = x^2 + 4x$
(a.) Does the graph open up or down?
(b.) What are the coordinates of the vertex?
(c.) What is the equation of the axis of symmetry?
(d.) Determine the intercepts.
(e.) Graph the function.
(f.) Determine the domain and the range.
(g.) Determine where the function is increasing and/or decreasing.
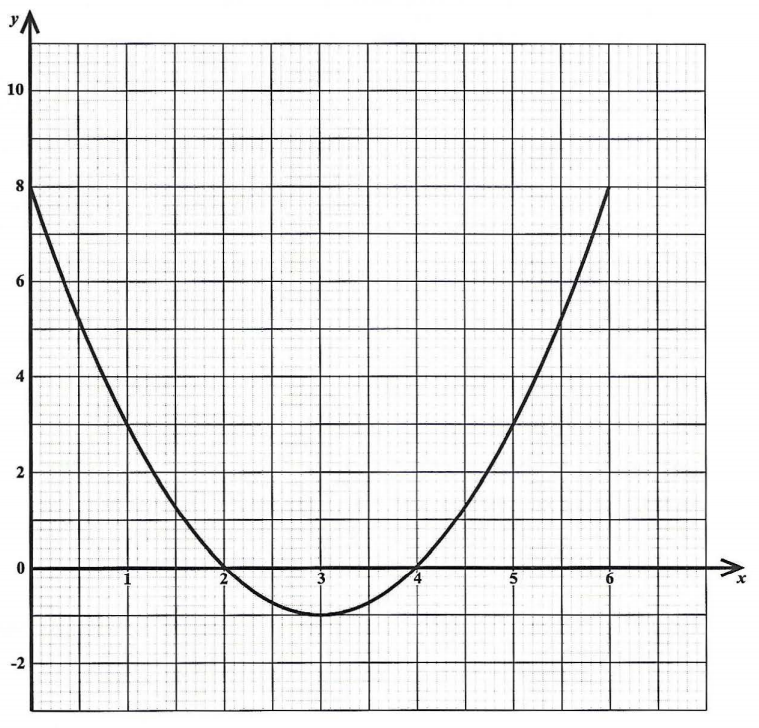
$ (a.) \\[3ex] f(x) = x^2 + 4x \\[3ex] Compare \\[3ex] f(x) = ax^2 + bx + c \\[3ex] a = 1 \\[3ex] 1 \gt 0 \\[3ex] Graph\;\;opens\;\;up \\[3ex] (b.) \\[3ex] a = 1 \\[3ex] b = 4 \\[3ex] x-coordinate\;\;of\;\;vertex = -\dfrac{b}{2a} = -\dfrac{4}{2(1)} = \dfrac{-4}{2} = -2 \\[5ex] y-coordinate\;\;of\;\;vertex = f(-2) = (-2)^2 + 4(-2) = 4 - 8 = -4 \\[3ex] vertex = \left(-\dfrac{b}{2a}, f(-\dfrac{b}{2a})\right) = (-2, -4) \\[5ex] (c.) \\[3ex] axis\;\;of\;\;symmetry:\;\; x = h \\[3ex] x = -2 \\[3ex] (d.) \\[3ex] \underline{x-intercept} \\[3ex] set\;\;y = 0\;\;and\;\;solve\;\;for\;\;x \\[3ex] f(x) = x^2 + 4x \\[3ex] x^2 + 4x = f(x) \\[3ex] x^2 + 4x = y \\[3ex] x^2 + 4x = 0 \\[3ex] x(x + 4) = 0 \\[3ex] x = 0 \;\;\;OR\;\;\; x + 4 = 0 \\[3ex] x = 0 \;\;\;OR\;\;\; x = -4 \\[3ex] x-intercepts = (0, 0) \;\;\;and\;\;\; (-4, 0) \\[3ex] \underline{y-intercept} \\[3ex] set\;\;x = 0\;\;and\;\;solve\;\;for\;\;y \\[3ex] f(0) = 0^2 + 4(0) \\[3ex] f(0) = 0 + 0 = 0 \\[3ex] y-intercept = (0, 0) \\[3ex] $ (e.) To graph this function in MML (MyMath Lab), we need two points.
The vertex is one point.
One of the x-intercepts is another point.
The graph of the quadratic function is:
(f.) From this graph:
The domain includes all real numbers of x
The lowest y-value is −4. It is included. It is the minimum value of y
There is no maximum value for y
Therefore, the range includes all real numbers of y from −4 (included) to ∞
$ D = (-\infty, \infty) \\[3ex] R = [-4, \infty) \\[3ex] (g.) \\[3ex] f(x) \uparrow \;\;for\;\; x \in (-2, \infty) \\[3ex] f(x) \downarrow \;\;for\;\; x \in (-\infty, -2) $
(a.) Does the graph open up or down?
(b.) What are the coordinates of the vertex?
(c.) What is the equation of the axis of symmetry?
(d.) Determine the intercepts.
(e.) Graph the function.
(f.) Determine the domain and the range.
(g.) Determine where the function is increasing and/or decreasing.
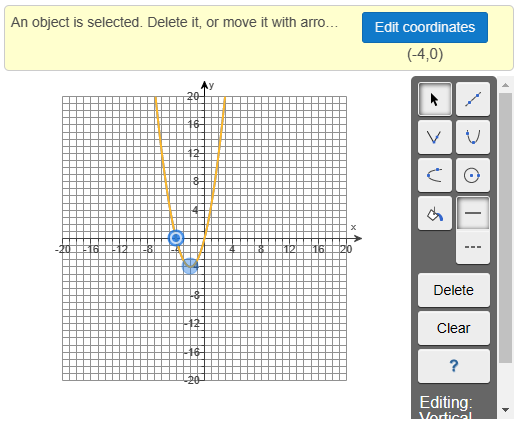
$ (a.) \\[3ex] f(x) = x^2 + 4x \\[3ex] Compare \\[3ex] f(x) = ax^2 + bx + c \\[3ex] a = 1 \\[3ex] 1 \gt 0 \\[3ex] Graph\;\;opens\;\;up \\[3ex] (b.) \\[3ex] a = 1 \\[3ex] b = 4 \\[3ex] x-coordinate\;\;of\;\;vertex = -\dfrac{b}{2a} = -\dfrac{4}{2(1)} = \dfrac{-4}{2} = -2 \\[5ex] y-coordinate\;\;of\;\;vertex = f(-2) = (-2)^2 + 4(-2) = 4 - 8 = -4 \\[3ex] vertex = \left(-\dfrac{b}{2a}, f(-\dfrac{b}{2a})\right) = (-2, -4) \\[5ex] (c.) \\[3ex] axis\;\;of\;\;symmetry:\;\; x = h \\[3ex] x = -2 \\[3ex] (d.) \\[3ex] \underline{x-intercept} \\[3ex] set\;\;y = 0\;\;and\;\;solve\;\;for\;\;x \\[3ex] f(x) = x^2 + 4x \\[3ex] x^2 + 4x = f(x) \\[3ex] x^2 + 4x = y \\[3ex] x^2 + 4x = 0 \\[3ex] x(x + 4) = 0 \\[3ex] x = 0 \;\;\;OR\;\;\; x + 4 = 0 \\[3ex] x = 0 \;\;\;OR\;\;\; x = -4 \\[3ex] x-intercepts = (0, 0) \;\;\;and\;\;\; (-4, 0) \\[3ex] \underline{y-intercept} \\[3ex] set\;\;x = 0\;\;and\;\;solve\;\;for\;\;y \\[3ex] f(0) = 0^2 + 4(0) \\[3ex] f(0) = 0 + 0 = 0 \\[3ex] y-intercept = (0, 0) \\[3ex] $ (e.) To graph this function in MML (MyMath Lab), we need two points.
The vertex is one point.
One of the x-intercepts is another point.
The graph of the quadratic function is:

(f.) From this graph:
The domain includes all real numbers of x
The lowest y-value is −4. It is included. It is the minimum value of y
There is no maximum value for y
Therefore, the range includes all real numbers of y from −4 (included) to ∞
$ D = (-\infty, \infty) \\[3ex] R = [-4, \infty) \\[3ex] (g.) \\[3ex] f(x) \uparrow \;\;for\;\; x \in (-2, \infty) \\[3ex] f(x) \downarrow \;\;for\;\; x \in (-\infty, -2) $
(4.) For the quadratic function: $f(x) = -x^2 - 4x$
(a.) Does the graph open up or down?
(b.) What are the coordinates of the vertex?
(c.) What is the equation of the axis of symmetry?
(d.) Determine the intercepts.
(e.) Graph the function.
(f.) Determine the domain and the range.
(g.) Determine where the function is increasing and/or decreasing.
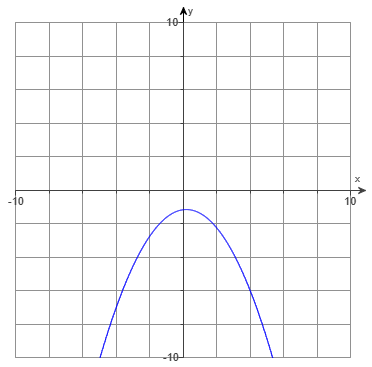
$ (a.) \\[3ex] f(x) = -x^2 - 4x \\[3ex] Compare \\[3ex] f(x) = ax^2 + bx + c \\[3ex] a = -1 \\[3ex] -1 \lt 0 \\[3ex] Graph\;\;opens\;\;down \\[3ex] (b.) \\[3ex] a = -1 \\[3ex] b = -4 \\[3ex] x-coordinate\;\;of\;\;vertex = -\dfrac{b}{2a} = -\dfrac{-4}{2(-1)} = \dfrac{4}{-2} = -2 \\[5ex] y-coordinate\;\;of\;\;vertex = f(-2) = -(-2)^2 - 4(-2) = -4 + 8 = 4 \\[3ex] vertex = \left(-\dfrac{b}{2a}, f(-\dfrac{b}{2a})\right) = (-2, 4) \\[5ex] (c.) \\[3ex] axis\;\;of\;\;symmetry:\;\; x = h \\[3ex] x = -2 \\[3ex] (d.) \\[3ex] \underline{x-intercept} \\[3ex] set\;\;y = 0\;\;and\;\;solve\;\;for\;\;x \\[3ex] f(x) = -x^2 - 4x \\[3ex] -x^2 - 4x = f(x) \\[3ex] -x^2 - 4x = y \\[3ex] -x^2 - 4x = 0 \\[3ex] -x(x + 4) = 0 \\[3ex] -x = 0 \;\;\;OR\;\;\; x + 4 = 0 \\[3ex] x = 0 \;\;\;OR\;\;\; x = -4 \\[3ex] x-intercepts = (0, 0) \;\;\;and\;\;\; (-4, 0) \\[3ex] \underline{y-intercept} \\[3ex] set\;\;x = 0\;\;and\;\;solve\;\;for\;\;y \\[3ex] f(0) = -0^2 - 4(0) \\[3ex] f(0) = -0 - 0 = 0 \\[3ex] y-intercept = (0, 0) \\[3ex] $ (e.) To graph this function in MML (MyMath Lab), we need two points.
The vertex is one point.
One of the x-intercepts is another point.
The graph of the quadratic function is:
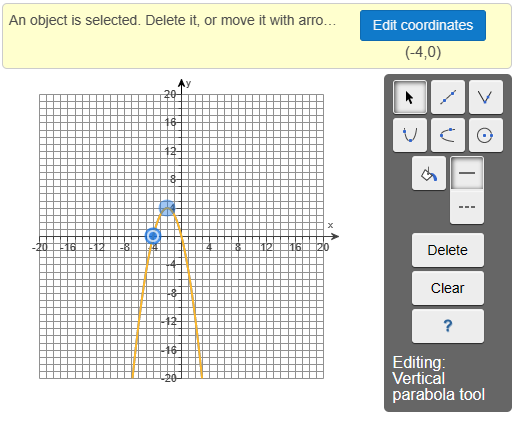
(f.) From this graph:
The domain includes all real numbers of x
The highest y-value is 4. It is included. It is the maximum value of y
There is no minimum value for y
Therefore, the range includes all real numbers of y from −∞ to 4 (included)
$ D = (-\infty, \infty) \\[3ex] R = (-\infty, 4] \\[3ex] (g.) \\[3ex] f(x) \uparrow \;\;for\;\; x \in (-\infty, -2) \\[3ex] f(x) \downarrow \;\;for\;\; x \in (-2, \infty) $
(a.) Does the graph open up or down?
(b.) What are the coordinates of the vertex?
(c.) What is the equation of the axis of symmetry?
(d.) Determine the intercepts.
(e.) Graph the function.
(f.) Determine the domain and the range.
(g.) Determine where the function is increasing and/or decreasing.
$ (a.) \\[3ex] f(x) = -x^2 - 4x \\[3ex] Compare \\[3ex] f(x) = ax^2 + bx + c \\[3ex] a = -1 \\[3ex] -1 \lt 0 \\[3ex] Graph\;\;opens\;\;down \\[3ex] (b.) \\[3ex] a = -1 \\[3ex] b = -4 \\[3ex] x-coordinate\;\;of\;\;vertex = -\dfrac{b}{2a} = -\dfrac{-4}{2(-1)} = \dfrac{4}{-2} = -2 \\[5ex] y-coordinate\;\;of\;\;vertex = f(-2) = -(-2)^2 - 4(-2) = -4 + 8 = 4 \\[3ex] vertex = \left(-\dfrac{b}{2a}, f(-\dfrac{b}{2a})\right) = (-2, 4) \\[5ex] (c.) \\[3ex] axis\;\;of\;\;symmetry:\;\; x = h \\[3ex] x = -2 \\[3ex] (d.) \\[3ex] \underline{x-intercept} \\[3ex] set\;\;y = 0\;\;and\;\;solve\;\;for\;\;x \\[3ex] f(x) = -x^2 - 4x \\[3ex] -x^2 - 4x = f(x) \\[3ex] -x^2 - 4x = y \\[3ex] -x^2 - 4x = 0 \\[3ex] -x(x + 4) = 0 \\[3ex] -x = 0 \;\;\;OR\;\;\; x + 4 = 0 \\[3ex] x = 0 \;\;\;OR\;\;\; x = -4 \\[3ex] x-intercepts = (0, 0) \;\;\;and\;\;\; (-4, 0) \\[3ex] \underline{y-intercept} \\[3ex] set\;\;x = 0\;\;and\;\;solve\;\;for\;\;y \\[3ex] f(0) = -0^2 - 4(0) \\[3ex] f(0) = -0 - 0 = 0 \\[3ex] y-intercept = (0, 0) \\[3ex] $ (e.) To graph this function in MML (MyMath Lab), we need two points.
The vertex is one point.
One of the x-intercepts is another point.
The graph of the quadratic function is:

(f.) From this graph:
The domain includes all real numbers of x
The highest y-value is 4. It is included. It is the maximum value of y
There is no minimum value for y
Therefore, the range includes all real numbers of y from −∞ to 4 (included)
$ D = (-\infty, \infty) \\[3ex] R = (-\infty, 4] \\[3ex] (g.) \\[3ex] f(x) \uparrow \;\;for\;\; x \in (-\infty, -2) \\[3ex] f(x) \downarrow \;\;for\;\; x \in (-2, \infty) $