Word Problems on Quadratic Functions

For ACT Students
The ACT is a timed exam...60 questions for 60 minutes
This implies that you have to solve each question in one minute.
Some questions will typically take less than a minute a solve.
Some questions will typically take more than a minute to solve.
The goal is to maximize your time. You use the time saved on those questions you solved in less than a minute, to solve the questions that will take more than a minute.
So, you should try to solve each question correctly and timely.
So, it is not just solving a question correctly, but solving it correctly on time.
Please ensure you attempt all ACT questions.
There is no negative penalty for a wrong answer.

For JAMB Students
Calculators are not allowed. So, the questions are solved in a way that does not require a calculator.

Solve all questions.
Show all work.

(1.) Be Good Technologies manufactures Smart TVs (television sets).
In order to avoid losses (loss prevention), the company is expected to manufacture up to two hundred TVs per work day per week.
A mathematician hired to study the business model of the company determined that the profit made from the sale of the TVs is modeled by the function:
$P(x) = -x^2 + 280x - 7500$
where:
$P(x)$ is the profit in dollars and
$x$ is the number of Smart TVs maufactured and sold.
Based on this model:

(a.) Determine the y-intercept
Explain your result.

(b.) Determine the x-intercept
Explain your result.

$ y = P(x) \\[3ex] P(x) = -x^2 + 280x - 7500 \\[3ex] P(x) = -1 * x^2 + 280x - 7500 \\[3ex] (a.)\;\;To\;\;determine\;\;y-intercept \\[3ex] Set\;\;x = 0 \\[3ex] Solve\;\;for\;\;P(0) \\[3ex] P(x) = -1 * 0^2 + 280(0) - 7500 \\[3ex] P(0) = -1(0) + 0 - 7500 \\[3ex] P(0) = 0 + 0 - 7500 \\[3ex] P(0) = -7500 \\[3ex] y-intercept = (0, -7500) \\[3ex] $ According to the business model, if no Smart TV is sold on any work day in any week, the company will lose $7500.00
Number 1(a.)

$ P(x) = -x^2 + 280x - 7500 \\[3ex] (b.)\;\;To\;\;determine\;\;x-intercept \\[3ex] Set\;\;P(x) = 0 \\[3ex] Solve\;\;for\;\;x \\[3ex] 0 = -x^2 + 280x - 7500 \\[3ex] -x^2 + 280x - 7500 = 0 \\[3ex] Divide\;\;both\;\;sides\;\;by\;\;-1 \\[3ex] x^2 - 280x + 7500 = 0 \\[3ex] x^2 - 250x - 30x + 7500 = 0 \\[3ex] x(x - 250) - 30(x - 250) = 0 \\[3ex] (x - 250)(x - 30) = 0 \\[3ex] x - 250 = 0 \;\;OR\;\; x - 30 = 0 \\[3ex] x = 250 \;\;OR\;\; x = 30 \\[3ex] x-intercepts\;\;are\;\; (30, 0) \;\;and\;\; (250, 0) \\[3ex] $ These are the zeros of the function.
According to the business model, the company will break even (make no profit or loss) if 30 TVs or 250 TVs are sold on any work day.
On any work day:
if less than 30 TVs are sold, the company will incur loss
if more than 250 TVs are sold, the company will also incur loss.
Number 1(b.)

(2.) MEHA A women's club makes mats and sells them for $73 each.
The cost, in dollars, of making x mats is given by $C(x) = 3.6x^2 + x$
(a) What is the cost of making 15 mats?
(b) Find the formula for the profit made by selling x mats.
(c) Determine the number of mats the club should produce and sell to maximise its profit.

$ C(x) = cost\;\;function \\[3ex] R(x) = revenue\;\;function \\[3ex] P(x) = profit\;\;function \\[3ex] (a) \\[3ex] C(x) = 3.6x^2 + x \\[3ex] C(15) = 3.6(15)^2 + 15 \\[3ex] C(15) = 3.6(225) + 15 \\[3ex] C(15) = \$825.00 \\[3ex] (b) \\[3ex] R(x) = 73 * x = 73x \\[3ex] P(x) = R(x) - C(x) \\[3ex] P(x) = 73x - (3.6x^2 + x) \\[3ex] P(x) = 73x - 3.6x^2 - x \\[3ex] P(x) = -3.6x^2 + 72x \\[3ex] (c) \\[3ex] $ We can solve this question part using at least two approaches.
Vertex Method: the x-coordinate of the vertex gives the number of mats that should be sold to maximise the profit.
The y-coordinate of the vertex gives the maximum profit.

$ \underline{Vertex\;\;Method} \\[3ex] P(x) = -3.6x^2 + 72x \\[3ex] a = -3.6,\;\; b = 72,\;\; c = 0 \\[3ex] x-coordinate\;\;of\;\;vertex \\[3ex] = -\dfrac{b}{2a} \\[5ex] = -\dfrac{72}{2(-3.6)} \\[5ex] = -\dfrac{72}{-7.2} \\[5ex] = 10 \\[3ex] $

10 mats should be produced and sold to maximise profit.
The maximum profit is $360.00

$ \underline{Differential\;\;Calculus\;\;Approach} \\[3ex] P(x) = -3.6x^2 + 72x \\[3ex] P'(x) = -7.2x + 72 \\[3ex] Set\;\;P'(x) = 0 \;\;and\;\;solve\;\;for\;\;x \\[3ex] -7.2x + 72 = 0 \\[3ex] -7.2x = -72 \\[3ex] x = \dfrac{-72}{-7.2} \\[5ex] x = 10 \\[3ex] $ 10 mats should be produced and sold to maximise profit.

(3.) The price p (in dollars) and the quantity x sold of a certain product satisfy the demand equation:
$x = -8p + 800$
(a.) Determine a model that expresses the revenue R as a function of p. (Hint: $R = xp$)
(b.) What is the domain of R?
(c.) What price maximizes the revenue?
(d.) What is the maximum revenue?
(e.) How many units are sold at this price?
(f.) Graph R.
(g.) What price should the company charge to earn at least $10,752 in revenue?

$ (a.) \\[3ex] x = -8p + 800 \\[3ex] R = xp \\[3ex] R(p) = p(-8p + 800) \\[3ex] R(p) = -8p^2 + 800p \\[3ex] $ (b.) The revenue cannot be negative.
The revenue can be zero (no revenue)
The revenue can be positive
Hence, the revenue must be nonnegative
The domain of R includes all the real number prices such that the revenue is nonnegative

$ R(p) \ge 0 \\[3ex] -8p^2 + 800p \ge 0 \\[3ex] -8(p^2 - 100p) \ge 0 \\[3ex] p^2 - 100p \le \dfrac{0}{-8} \\[5ex] p^2 - 100p \le 0 \\[3ex] p(p - 100) \le 0 \\[3ex] Assume:\;\;p(p - 100) = 0 \\[3ex] p = 0 \;\;\;OR\;\;\; p - 100 = 0 \\[3ex] p = 0 \;\;\;OR\;\;\; p = 100 \\[3ex] Test\;\;Intervals\;\;are: \\[3ex] p \lt 0 \\[3ex] 0 \le p \le 100 \\[3ex] p \gt 100 \\[3ex] $

Let:	p < 0 p = −1	0 ≤ p ≤ 100 p = 1	p > 0 p = 101
$p$	−	+	+
$p - 100$	−	−	+
$p(p - 100)$	+	−	+

Less than or equal to zero means nonnegative
Hence, the second test interval gives the solution of the inequality
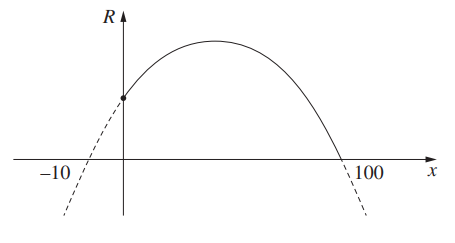
Domain, D = {p | 0 ≤ p ≤ 100}

(c.) The price that maximizes revenue is the xx-coordinate of the revenue function.

$ R(p) = -8p^2 + 800p \\[3ex] Compare:\;\;R(p) = ap^2 + bp + c \\[3ex] a = -8 \\[3ex] b = 800 \\[3ex] x-coordinate\;\;of\;\;vertex = -\dfrac{b}{2a} \\[5ex] p = \dfrac{-800}{2(-8)} \\[5ex] = \dfrac{-800}{-16} \\[5ex] = 50 \\[3ex] $ The price that maximizes revenue is $50

(d.) The maximum revenue is the y-coordinate of the vertex

$ R(p) = -8p^2 + 800p \\[3ex] p = \$50 \\[3ex] y-coordinate\;\;of\;\;vertex = R(50) \\[3ex] R(50) = -8(50)^2 + 800(50) \\[3ex] = -8(2500) + 40000 \\[3ex] = -20000 + 40000 \\[3ex] = 20000 \\[3ex] $ The maximum revenue is $20,000

(e.) The number of units sold at this price is the value of x for which R = $20000

$ vertex = (x, y) = (p, R) = (50, 20000) \\[3ex] R = xp \\[3ex] xp = R \\[3ex] x = \dfrac{R}{p} \\[5ex] x = \dfrac{20000}{50} \\[5ex] x = 400 \\[3ex] $ 400 units were sold at the price that gave the maximum revenue.

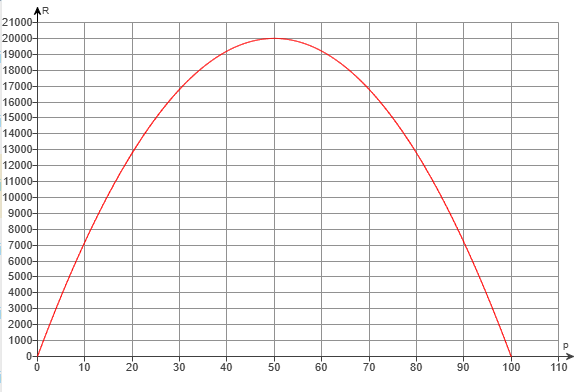
(f.) The graph of the revenue versus price is shown below.
Keep in mind that the vertex is (p, R) = (50, 20000)

Number 3

(g.) The price that the company should charge to earn at least $10,752

At least 10752 means ≥ 10752
They are asking us to determine the price range for which the revenue is greater than or equal to $10,752

$ -8p^2 + 800p \ge 10752 \\[3ex] -8p^2 + 800p - 10752 \ge 0 \\[3ex] -8(p^2 - 100p + 1344) \ge 0 \\[3ex] p^2 - 100p + 1344 \le \dfrac{0}{-8} \\[5ex] p^2 - 100p + 1344 \le 0 \\[3ex] (p - 16)(p - 84) \le 0 \\[3ex] Assume:\;\;(p - 16)(p - 84) = 0 \\[3ex] p - 16 = 0 \;\;\;OR\;\;\; p - 84 = 0 \\[3ex] p = 16 \;\;\;OR\;\;\; p = 84 \\[3ex] Test\;\;Intervals\;\;are: \\[3ex] p \lt 16 \\[3ex] 16 \le p \le 84 \\[3ex] p \gt 84 \\[3ex] $

Let:	p < 16 p = 0	16 ≤ p ≤ 84 p = 17	p > 84 p = 85
$p - 16$	−	+	+
$p - 84$	−	−	+
$(p - 16)(p - 84)$	+	−	+

Less than or equal to zero means nonnegative
Hence, the second test interval gives the solution of the inequality
The solution is: {p | 16 ≤ p ≤ 84}
The company should a price between a minimum of $16.00 and a maximum of $84.00

(5.) A ball is thrown directly upward from a height of 2 ft with an initial velocity of 28 ft/sec.
The function: $h(t) = -16t^2 + 28t + 2$ gives the height of the ball in feet, t seconds after it has been thrown.
(a.) Determine the time at which the ball reaches its maximum height.
(b.) Calculate the maximum height.

Notice the bold letter maximum in the question
The question is asking for the vertex

$ h(t) = -16t^2 + 28t + 2 \\[3ex] f(x) = ax^2 + bx + c \\[3ex] a = -16, b = 28, c = 2 \\[3ex] Vertex = \left(-\dfrac{b}{2a}, f\left(-\dfrac{b}{2a}\right)\right) \\[5ex] -\dfrac{b}{2a} = -\dfrac{28}{2(-16)} \\[5ex] -\dfrac{b}{2a} = \dfrac{-28}{-32} = \dfrac{7}{8} \\[5ex] f\left(-\dfrac{b}{2a}\right) = f\left(\dfrac{7}{8}\right) \\[5ex] But\:\: h(t) = -16t^2 + 28t + 2 \\[3ex] h\left(\dfrac{7}{8}\right) = -16\left(\dfrac{7}{8}\right)^2 + 28\left(\dfrac{7}{8}\right) + 2 \\[5ex] h\left(\dfrac{7}{8}\right) = -16\left(\dfrac{7}{8}\right)\left(\dfrac{7}{8}\right) + 7\left(\dfrac{7}{2}\right) + 2 \\[5ex] h\left(\dfrac{7}{8}\right) = -2\left(\dfrac{7}{1}\right)\left(\dfrac{7}{8}\right) + \dfrac{49}{2} + 2 \\[5ex] h\left(\dfrac{7}{8}\right) = -1\left(\dfrac{7}{1}\right)\left(\dfrac{7}{4}\right) + \dfrac{49}{2} + 2 \\[5ex] h\left(\dfrac{7}{8}\right) = -\dfrac{49}{4} + \dfrac{49}{2} + 2 \\[5ex] h\left(\dfrac{7}{8}\right) = -\dfrac{49}{4} + \dfrac{98}{4} + \dfrac{8}{4} \\[5ex] h\left(\dfrac{7}{8}\right) = \dfrac{-49 + 98 + 8}{4} \\[5ex] h\left(\dfrac{7}{8}\right) = \dfrac{57}{4} \\[5ex] h\left(\dfrac{7}{8}\right) = \dfrac{57}{4} \\[5ex] $

The time to reach the maximum height is $\dfrac{7}{8} = 0.875$ seconds

The maximum height is $\dfrac{57}{4} = 14.25$ feet

(6.) JAMB A trader realizes $10x - x^2$ naira profit from the sale of x bags of corn.
How many bags will give him the maximum profit?

$ A.\;\; 4 \\[3ex] B.\;\; 5 \\[3ex] C.\;\; 6 \\[3ex] D.\;\; 7 \\[3ex] $

We can do this question in at least two ways.
You may use any of the methods to solve it.

First Method: Vertex Formula: this is because the profit is a quadratic function
For this question:
the number of bags that will give the maximum profit = $x$ coordinate of the vertex
the maximum profit = $y$ coordinate of the vertex

$ y = 10x - x^2 \\[3ex] y = -x^2 + 10x \\[3ex] y = ax^2 + bx + c \\[3ex] a = -1, b = 10 \\[3ex] x-coordinate\:\: of\:\: Vertex = -\dfrac{b}{2a} \\[5ex] = \dfrac{-10}{2(-1)} \\[5ex] = \dfrac{-10}{-2} \\[5ex] = 5 \\[3ex] $ The sale of 5 bags will give the maximum profit.
The maximum profit is 25 naira.

Second Method: Differential Calculus
One of the application of derivatives is in calculating maxima and minima of functions
$ y = 10x - x^2 \\[3ex] \dfrac{dy}{dx} = 10 - 2x \\[3ex] 10 - 2x = 0 \\[3ex] 10 = 2x \\[3ex] 2x = 10 \\[3ex] x = \dfrac{10}{2} \\[3ex] x = 5 \\[3ex] $ The sale of 5 bags will give the maximum profit.

(8.) ACT The CFO of Math King Enterprises estimates that if the company sets a price of c cents for each unit of their new product, then the weekly profit from selling the product will be modeled by $p(c) = 1,600c - 4c^2$, where $0 \le c \le 400$
According to the this model, for which of the following values of c will the weekly profit for this product be the largest?

$ A.\;\; 20 \\[3ex] B.\;\; 40 \\[3ex] C.\;\; 100 \\[3ex] D.\;\; 200 \\[3ex] E.\;\; 400 \\[3ex] $

This is an application of the vertex: ... values of $c$ will the weekly profit for this product be the largest?
This question requires us to find the $x-component$ of the vertex
The $x-component$ of the vertex is the price that will give the largest weekly profit
The $y-component$ of the vertex is the largest weekly profit

$ p(c) = 1,600c - 4c^2 \\[3ex] p(c) = -4c^2 + 1600c \\[3ex] Compare\;\;to\;\; ax^2 + bx + c \\[3ex] a = -4 \\[3ex] b = 1600 \\[3ex] c = 0 \\[3ex] $ This is not the actual value of $c$
It is the comparison to the standard form.
Anyway, we do not need the value of $c$ for this question.

$ x-component\;\;of\;\;vertex \\[3ex] = -\dfrac{b}{2a} \\[5ex] = -\dfrac{1600}{2(-4)} \\[5ex] = -\dfrac{1600}{-8} \\[5ex] = 200 \\[3ex] $

Based on the function: $p(c) = 1,600c - 4c^2$, the company needs to set the price at 200 cents for each unit of their new product in order to earn the largest weekly profit.

(10.) Based on Question (8.)
According to the model, what value of c will the company break even for the weekly sales of the product?

The question wants us to find the zeros of the function.

$ p(c) = 1,600c - 4c^2 \\[3ex] p(c) = -4c^2 + 1600c \\[3ex] Set\;\;p(c) = 0 \;\;and\;\;solve\;\;for\;\;c \\[3ex] 0 = -4c^2 + 1600c \\[3ex] -4c^2 + 1600c = 0 \\[3ex] -4c(c - 400) = 0 \\[3ex] -4c = 0 \;\;OR\;\; c - 400 = 0 \\[3ex] c = \dfrac{0}{-4} \;\;OR\;\; c = 0 + 400 \\[5ex] c = 0 \;\;OR\;\; c = 400 \\[3ex] $ Because the company cannot set the price at 0 cents (technically) because the employees most likely do not work for free, the company will break even (make no profit or loss) if the price of each unit of their new product is set at 400 cents.

(13.) ACT A sporting-goods store sells baseball caps for $22 each.
At this price, 40 caps are sold per week.
For every $1 decrease in price, the store will sell 4 more caps per week.
The store will adjust the price to maximize revenue.
What will be the maximum possible revenue for 1 week?
(Note: The revenue equals the number of caps sold times the price per cap.)

Normal revenue for 1 week = $40 * 22 = \$880$
But, the store wants to make more money.
For every $\$1$ decrease in price, the store will sell $4$ more caps per week.
For $22 - 1 = 21$, the store will sell $40 + 4 = 44$ caps
The company will sell $4$ more caps for a $\$1$ decrease in price
Revenue would be $21 * 44 = \$924$
For $22 - 1(2) = 20$, the store will sell $40 + 4(2) = 40 + 8 = 48$ caps
The company will sell $8$ more caps for a $\$2$ decrease in price
Revenue would be $20 * 48 = \$960$
For $22 - 1(3) = 19$, the store will sell $40 + 4(3) = 40 + 12 = 52$ caps
The company will sell $12$ more caps for a $\$3$ decrease in price
Revenue would be $19 * 52 = \$988$

Student: That would exactly take more than a minute to solve.
ACT questions typically should be solved at at an average of $1$ question per minute.
Teacher: I expected that comment.
I did those steps to explain the question to you.
I was doing it the Arithmetic method.
Let us now do it algebraically.

So;
For each $\$x$ decrease in price, the company will sell $4x$ more
For $22 - 1(x) = 22 - x$, the store will sell $40 + 4(x) = 40 + 4x$ caps
Revenue would be $(22 - x) * (40 + 4x)$
Let Revenue = $R$

$ R = (22 - x)(40 + 4x) \\[3ex] = 880 + 88x - 40x - 4x^2 \\[3ex] = 880 + 48x - 4x^2 \\[3ex] = -4x^2 + 48x + 880 \\[3ex] R = -4x^2 + 48x + 880 \\[3ex] y = ax^2 + bx + c \\[3ex] a = -4, b = 48 \\[3ex] x-coordinate\:\: of\:\: vertex = -\dfrac{b}{2a} \\[5ex] = -\dfrac{48}{2(-4)} = \dfrac{-48}{-8} = 6 \\[5ex] $ The store has to decrease the price by $\$6$
This means that the store has to sell each cap for $22 - 6 = \$16$
By doing so, the store will sell $40 + 4(6) = 40 + 24 = 64$ caps
Revenue = $16 * 64 = \$1024$

Student: So, this is the maximum revenue the store can get?
Teacher: That is correct.
Student: What if the store sells each cap for $\$15$?
Teacher: Go ahead and find the revenue
Student: Okay...it will be
$15 * (64 + 4) = 15 * 68 = \$1020$
Interesting application of Quadratic Functions!

(14.) HSC A publisher sells a book for $10.
At this price, 5000 copies of the book will be sold and the revenue raised will be 5000 * 10 = $50 000.
The publisher is considering increasing the price of the book.
For every dollar the price of the book is increased, the publisher will sell 50 fewer copies of the book.
If the publisher charges (10 + x) dollars for each book, a quadratic model for the revenue raised, R, from selling the books is $$ R = -50x^2 + 4500x + 50 000. $$ A graph of this quadratic model for revenue is shown.
A dashed line is used for values of x which are not relevant to the practical context of this problem.

(a) By first finding a suitable value of x, find the price the publisher should charge for each book to maximise the revenue raised from sales of the book.

(b) Find the value of the intercept of the parabola with the vertical axis.

The price to maximise the revenue is the xx-coordinate of the vertex
The maximum revenue is the y-coordinate of the vertex.

$ (a) \\[3ex] R = -50x^2 + 4500x + 50 000 \\[3ex] a = -50 \\[3ex] b = 4500 \\[3ex] x-coordinate\;\;of\;\;the\;\;vertex \\[3ex] = -\dfrac{b}{2a} \\[5ex] = - \dfrac{4500}{2(-50)} \\[5ex] = \dfrac{-4500}{-100} \\[5ex] = 45 \\[3ex] $ However, we noticed from the graph that 10 units of x was cut off
To account for those units due to symmetry, we should add 10 to the value of x
Therefore, the price to maximise revenue = 45 + 10 = $55.00

(b)
To find the value of the intercept of the parabola with the vertical axis means that we should find the y-intercept
To find the y-intercept, set the value of x to be zero and solve for y

$ R = -50x^2 + 4500x + 50 000 \\[3ex] set\;\;x = 0 \\[3ex] \implies \\[3ex] R = -50(0)^2 + 4500(0) + 50 000 \\[3ex] R = 0 + 0 + 50000 \\[3ex] R = \$50000.00 \\[3ex] $ The value of the intercept of the parabola with the vertical axis is $50 000.00

Top